
【題目】如圖,正方形![]() 的邊
的邊![]() 在正方形
在正方形![]() 的邊
的邊![]() 上,連結(jié)
上,連結(jié)![]() 、
、![]() .
.
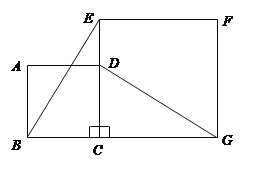
(1)觀察猜想![]() 與
與![]() 之間的大小關(guān)系,并證明你的結(jié)論;
之間的大小關(guān)系,并證明你的結(jié)論;
(2)圖中是否存在通過旋轉(zhuǎn)能夠互相重合的兩個(gè)三角形?若存在,說出旋轉(zhuǎn)過程;若不存在,請(qǐng)說明理由.
 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
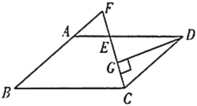
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分線交
的平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,則
,則![]() 的周長(zhǎng)為_______.
的周長(zhǎng)為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我市某社區(qū)今年準(zhǔn)備新建一養(yǎng)老中心,其中規(guī)劃建造三類養(yǎng)老專用房間共100間,這三類養(yǎng)老專用房間分別為單人間(1個(gè)養(yǎng)老床位),雙人間(2個(gè)養(yǎng)老床位),三人間(3個(gè)養(yǎng)老床位),因?qū)嶋H需要,單人間房間數(shù)在10至30之間(包括10和30),且雙人間的房間數(shù)是單人間的2倍,設(shè)規(guī)劃建造單人間的房間數(shù)為![]() .
.
(1)根據(jù)題意,填寫下表:
單人間的房間數(shù) | 10 | … |
| … | 30 |
雙人間的房間數(shù) | _________ | … |
| … | 60 |
三人間的房間數(shù) | 70 | … | _________ | … | _________ |
養(yǎng)老床位數(shù) | 260 | … | _________ | … | _________ |
(2)若該養(yǎng)老中心建成后可提供養(yǎng)老床位200個(gè),求![]() 的值;
的值;
(3)求該養(yǎng)老中心建成后最多提供養(yǎng)老床位多少個(gè)?最少提供養(yǎng)老床位多少個(gè)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩個(gè)草莓采摘園為吸引顧客,在草莓銷售價(jià)格相同的基礎(chǔ)上分別推出優(yōu)惠方案,甲園:顧客進(jìn)園需購買門票,采摘的草莓按六折優(yōu)惠.乙園:顧客進(jìn)園免門票,采摘草莓超過一定數(shù)量后,超過的部分打折銷售.活動(dòng)期間,某顧客的草莓采摘量為x kg,若在甲園采摘需總費(fèi)用y1元,若在乙園采摘需總費(fèi)用y2元, y1,y2與x之間的函數(shù)圖象如圖所示,則下列說法中錯(cuò)誤的是( )
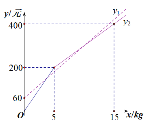
A.甲園的門票費(fèi)用是60元
B.草莓優(yōu)惠前的銷售價(jià)格是40元/kg
C.乙園超過5 kg后,超過的部分價(jià)格優(yōu)惠是打五折
D.若顧客采摘12 kg草莓,那么到甲園或乙園的總費(fèi)用相同
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
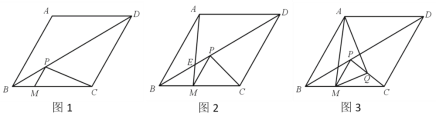
【題目】已知菱形ABCD中,∠ABC=60°,AB=4,點(diǎn)M在BC邊上,過點(diǎn)M作PM∥AB交對(duì)角線BD于點(diǎn)P,連接PC.
(1)如圖1,當(dāng)BM=1時(shí),求PC的長(zhǎng);
(2)如圖2,設(shè)AM與BD交于點(diǎn)E,當(dāng)∠PCM=45°時(shí),求證:![]() =
=![]() ;
;
(3)如圖3,取PC的中點(diǎn)Q,連接MQ,AQ.
①請(qǐng)?zhí)骄?/span>AQ和MQ之間的數(shù)量關(guān)系,并寫出探究過程;
②△AMQ的面積有最小值嗎?如果有,請(qǐng)直接寫出這個(gè)最小值;如果沒有,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
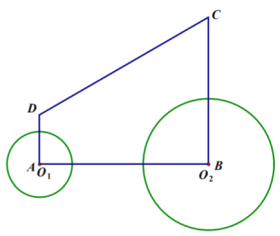
【題目】如圖,直角梯形![]() 中,
中,![]() 的圓心
的圓心![]() 從點(diǎn)
從點(diǎn)![]() 開始沿折線
開始沿折線![]() 以
以![]() 的速度向點(diǎn)
的速度向點(diǎn)![]() 運(yùn)動(dòng),
運(yùn)動(dòng),![]() 的圓心
的圓心![]() 從點(diǎn)
從點(diǎn)![]() 開始沿
開始沿![]() 邊以
邊以![]()
![]() 的速度向點(diǎn)
的速度向點(diǎn)![]() 運(yùn)動(dòng),
運(yùn)動(dòng),![]() 半徑為
半徑為![]() 的半徑為
的半徑為![]() ,若
,若![]() 分別從點(diǎn)
分別從點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 同時(shí)出發(fā),運(yùn)動(dòng)的時(shí)間為
同時(shí)出發(fā),運(yùn)動(dòng)的時(shí)間為![]()
(1)請(qǐng)求出![]() 與腰
與腰![]() 相切時(shí)
相切時(shí)![]() 的值;
的值;
(2)在![]() 范圍內(nèi),當(dāng)
范圍內(nèi),當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 與
與![]() 外切?
外切?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于A(-1,0)和B(3,0)兩點(diǎn),與y軸交于點(diǎn)C,對(duì)稱軸與x軸交于點(diǎn)E,點(diǎn)D為頂點(diǎn),連接BD、CD、BC.
與x軸交于A(-1,0)和B(3,0)兩點(diǎn),與y軸交于點(diǎn)C,對(duì)稱軸與x軸交于點(diǎn)E,點(diǎn)D為頂點(diǎn),連接BD、CD、BC.

(1)求證△BCD是直角三角形;
(2)點(diǎn)P為線段BD上一點(diǎn),若∠PCO+∠CDB=180°,求點(diǎn)P的坐標(biāo);
(3)點(diǎn)M為拋物線上一點(diǎn),作MN⊥CD,交直線CD于點(diǎn)N,若∠CMN=∠BDE,請(qǐng)直接寫出所有符合條件的點(diǎn)M的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
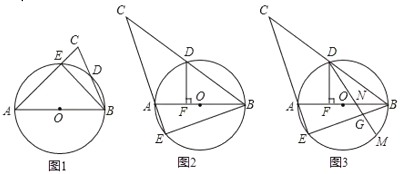
【題目】如圖,在![]() 中,以
中,以![]() 為直徑的
為直徑的![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() .
.
![]() 如圖1,求證:
如圖1,求證:![]() ;
;
![]() 如圖2,
如圖2,![]() 為鈍角時(shí),過點(diǎn)
為鈍角時(shí),過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() 求證:
求證:![]() ;
;
![]() 如圖3,在
如圖3,在![]() 的條件下,在∠BDF的內(nèi)部作
的條件下,在∠BDF的內(nèi)部作![]() ,使
,使![]() 分別交
分別交![]() 于點(diǎn)
于點(diǎn)![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,Rt△ABC中,點(diǎn)D,E分別為直角邊AC,BC上的點(diǎn),若滿足AD2+BE2=DE2,則稱DE為R△ABC的“完美分割線”.顯然,當(dāng)DE為△ABC的中位線時(shí),DE是△ABC的一條完美分割線.
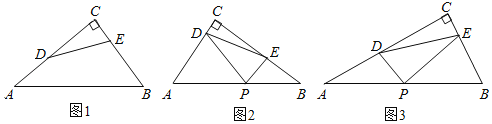
(1)如圖1,AB=10,cosA=![]() ,AD=3,若DE為完美分割線,則BE的長(zhǎng)是 .
,AD=3,若DE為完美分割線,則BE的長(zhǎng)是 .
(2)如圖2,對(duì)AC邊上的點(diǎn)D,在Rt△ABC中的斜邊AB上取點(diǎn)P,使得DP=DA,過點(diǎn)P畫PE⊥PD交BC于點(diǎn)E,連結(jié)DE,求證:DE是直角△ABC的完美分割線.
(3)如圖3,在Rt△ABC中,AC=10,BC=5,DE是其完美分割線,點(diǎn)P是斜邊AB的中點(diǎn),連結(jié)PD、PE,求cos∠PDE的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com