【題目】在平面直角坐標系中有兩點A（-2,2），B（1,4），根據要求求出P點的坐標：
（1）在x軸上找一點P，使得
最小
（2）在y軸上找一點P，使得最小
（3）在x軸上找一點P，使得
最大
（4）在x軸上找一點P，使得最小
【答案】（1）
；（2）
；（3）
；（4）
【解析】
試題分析：
（1）由于兩點間線段最短，故作A關于x軸的對稱點A’，連接A’B與x軸相交于點P，
則點P即為試PA+PB最短的點
（2）由于兩點間線段最短，故連接AB交y軸于P，則點P即為使PA+PB最短的點
（3）連接BA并延長交x軸于P，則點P即為使
最大的點
（4）因為
，所以當
，時
最小，即點
最小在
最小的垂直平分線上
試題解析：
解：（1）如下圖，作A關于x軸的對稱點A’，連接A’B與x軸相交于點P，
則點P即為試PA+PB最短的點
∵A（-2,2）
∴A’（-2，-2）
設直線A’B的解析式為：
∴
∴
∴直線A’B的解析式為：
當
時，
∴
（2）如下圖，連接AB交y軸于P，則點P即為使PA+PB最短的點
設直線AB的解析式為：
∴
∴
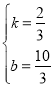
∴直線A’B的解析式為：
當
時，
∴
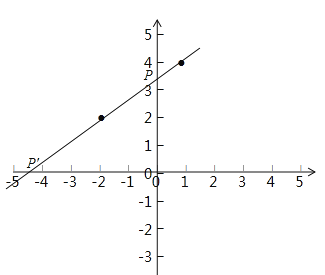
（3）連接BA并延長交x軸于
，則點
即為使最大的點
由（2）得直線AB的解析式為：
當y=0時，
∴
（4）如圖，∵
，
∴當AP=BP時，
最小
故點P在線段AB的垂直平分線上，作線段AB的垂直平分線交x軸于點P，
則點P即為所求
設P（x，0），則PA’=PB
即
解得:
故點P的坐標為
激活思維智能訓練課時導學練系列答案科目：初中數學 來源： 題型：
【題目】求數的方根，可以用估算的方法，但是這樣求方根速度太慢，計算器可以幫你解決這一問題，使你的計算快速大大加快，為此，熟練掌握用計算器求平方根和立方根的程序是關鍵．在計算器上，按程序2ndx2625）enter計算，顯示的結果是（ ）
A.25 B.±25 C.﹣25 D.15
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若∠A與∠B的兩邊分別垂直，請判斷這兩個角的等量關系．
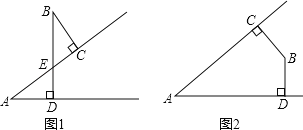
（1）如圖1，∠A與∠B的關系是 ；如圖2，∠A與∠B的關系是 ；
（2）若∠A與∠B的兩邊分別平行，試探索這兩個角的等量關系，畫圖并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】推理填空：
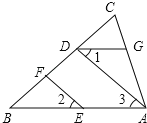
如圖，EF∥AD，∠1=∠2，∠BAC=70°．將求∠AGD的過程填寫完整．
因為EF∥AD，
所以∠2= ．（ ）
又因為∠1=∠2，
所以∠1=∠3．（ ）
所以AB∥ ．（ ）
所以∠BAC+ =180°（ ）
又因為∠BAC=70°，
所以∠AGD= ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了解“課程選修”的情況，對報名參加“藝術鑒賞”，“科技制作”，“數學思維”，“閱讀寫作”這四個選修項目的學生（每人限報一課）進行抽樣調查，下面是根據收集的數據繪制的不完整的統計圖，請根據圖中提供的信息，解答下面的問題：
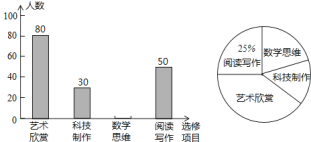
（1）此次共調查了______名學生，扇形統計圖中“藝術鑒賞”部分的圓心角是______度；
（2）請把這個條形統計圖補充完整；
（3）現該校共有800名學生報名參加這四個選修項目，請你估計其中有多少名學生選修“科技制作”項目．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將內直徑為20cm的圓柱形水桶中的全部水倒入一個長、寬、高分別為30cm，20cm，62.8cm的長方體鐵盒中，正好倒滿，求圓柱形水桶的高．（π取3.14）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某制藥廠兩年前生產1噸某種藥品的成本是100萬元，隨著生產技術的進步，現在生產1噸這種藥品的成本為81萬元．則這種藥品的成本的年平均下降率為%．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面說法錯誤的是 ( )
A. 三角形的三條角平分線交于一點 B. 三角形的三條中線交于一點
C. 三角形的三條高交于一點 D. 三角形的三條高所在的直線交于一點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com