
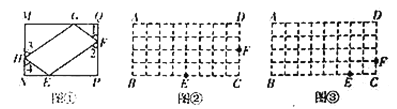
【題目】(問題原型)在圖①的矩形![]() 中,點
中,點![]() 、
、![]() 、
、![]() 、
、![]() 分別在
分別在![]() 、
、![]() 、
、![]() 、
、![]() 上,若
上,若![]() ,則稱四邊形
,則稱四邊形![]() 為矩形
為矩形![]() 的反射四邊形;
的反射四邊形;
(操作與探索)在圖②,圖③的矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 邊的格點上,試利用正方形網格分別在圖②、圖③上作矩形
邊的格點上,試利用正方形網格分別在圖②、圖③上作矩形![]() 的反射四邊形
的反射四邊形![]() ;
;
(發現與應用)由前面的操作可以發現,一個矩形有不同的反射四邊形,且這些反射四邊形的周長都相等.若在圖①的矩形![]() 中,
中,![]() ,
,![]() ,則其反射四邊形
,則其反射四邊形![]() 的周長為______.
的周長為______.
【答案】操作與探索:見解析:發現與應用:10.
【解析】
(1)根據網格作出相等的角即可得到反射四邊形;
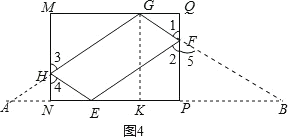
(2)延長GH交PN的延長線與點A,證明△FPE≌△FPB,根據全等三角形的性質得到AB=2NP,再證明GA=GB,過點G作GK⊥NP于K,根據等腰三角形的性質求出KB=![]() AB=4,再利用勾股定理求出GB的長,即可求出四邊形EFGH的周長.
AB=4,再利用勾股定理求出GB的長,即可求出四邊形EFGH的周長.
(1)作圖如下:
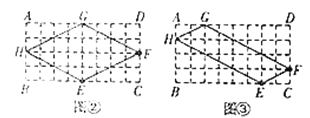
(2)延長GH交PN的延長線與點A,過點G作GK⊥NP于K,
∵∠1=∠2,∠1=∠5,∴∠2=∠5,
又PF=PF,∠FPE=∠FPB,
∴△FPE≌△FPB,
∴EF=BF,EP=PB,
同理AH=EH,NA=EN,
∴AB=2NP=8,
∵∠B=90°-∠5=90°-∠1,∠A=90°-∠3,
∴∠A=∠B,∴GA=GB,
則KB=![]() AB=4,∴GB=
AB=4,∴GB=![]()
∴四邊形EFGH的周長為2GB=10.


科目:初中數學 來源: 題型:
【題目】某政府在廣場上樹立了如圖所示的宣傳牌,數學興趣小組的同學想利用所學的知識測量宣傳牌的高度AB,在D處測得點A、B的仰角分別為38°、21°,已知CD=20m,點A、B、C在一條直線上,AC⊥DC,求宣傳牌的高度AB(sin21°≈0.36,cos21°≈0.93,tan21°≈0.38,sin38°≈0.62,cos38°≈0.78,tan38°≈0.79,結果精確到1米)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綠谷商場“家電下鄉”指定型號冰箱、彩電的進價和售價如下表所示:
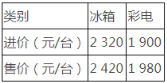
(1)按國家政策,農民購買“家電下鄉”產品可享受售價13%的政府補貼.農民田大伯到該商場購買了冰箱、彩電各一臺,可以享受多少元的政府補貼?
(2)為滿足農民需求,商場決定用不超過85000元采購冰箱、彩電共40臺,且冰箱的數量不少于彩電數量的![]() .
.
①請你幫助該商場設計相應的進貨方案;
②哪種進貨方案商場獲得利潤最大(利潤=售價-進價),最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
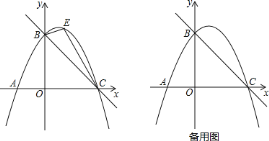
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過
經過![]() 、
、![]() 兩點.
兩點.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 如圖,點
如圖,點![]() 是直線
是直線![]() 上方拋物線上的一動點,當
上方拋物線上的一動點,當![]() 面積最大時,請求出點
面積最大時,請求出點![]() 的坐標和
的坐標和![]() 面積的最大值?
面積的最大值?
![]() 在
在![]() 的結論下,過點
的結論下,過點![]() 作
作![]() 軸的平行線交直線
軸的平行線交直線![]() 于點
于點![]() ,連接
,連接![]() ,點
,點![]() 是拋物線對稱軸上的動點,在拋物線上是否存在點
是拋物線對稱軸上的動點,在拋物線上是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是平行四邊形?如果存在,請直接寫出點
為頂點的四邊形是平行四邊形?如果存在,請直接寫出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
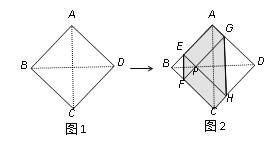
【題目】如圖1,正方形紙片ABCD的邊長為2,翻折∠B、∠D,使兩個直角的頂點重合于對角線BD上一點P、EF、GH分別是折痕(如圖2).設AE=x(0<x<2),給出下列判斷:①當x=1時,點P是正方形ABCD的中心;②當x=![]() 時,EF+GH>AC;③當0<x<2時,六邊形AEFCHG面積的最大值是3;④當0<x<2時,六邊形AEFCHG周長的值不變.其中正確的選項是( )
時,EF+GH>AC;③當0<x<2時,六邊形AEFCHG面積的最大值是3;④當0<x<2時,六邊形AEFCHG周長的值不變.其中正確的選項是( )
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寓言故事《烏鴉喝水》教導我們遇到困難要運用智慧、認真思考才能讓問題迎刃而解.如圖,一個緊口瓶中盛有一些水,可烏鴉的嘴夠不到瓶中的水.于是烏鴉銜來一些小石子放入瓶中,瓶中的水面高度得到提升.由于放入的石子較多,水都快溢出來了,烏鴉成功喝到了水,如果銜入瓶中石子的體積為![]() ,水面高度為
,水面高度為![]() ,下面圖象能大致表示該故事情節的是( )
,下面圖象能大致表示該故事情節的是( )
A.  B.
B. 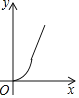 C.
C. 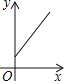 D.
D. 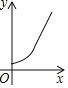
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡,再求值:
(1)2m2-4m+1-2(m2+2m-![]() ),其中m=-1;
),其中m=-1;
(2)5xy2-[2x2y-(2x2y-3xy2)],其中(x-2)2+|y+1|=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知識再現:
如果![]() ,
,![]() ,則線段
,則線段![]() 的中點坐標為
的中點坐標為![]() ;對于兩個一次函數
;對于兩個一次函數![]() 和
和![]() ,若兩個一次函數圖象平行,則
,若兩個一次函數圖象平行,則![]() 且
且![]() ;若兩個一次函數圖象垂直,則
;若兩個一次函數圖象垂直,則![]() .
.
提醒:在下面這個相關問題中如果需要,你可以直接利用以上知識.
在平面直角坐標系中,已知點![]() ,
,![]() .
.
(1)如圖1,把直線![]() 向右平移使它經過點
向右平移使它經過點![]() ,如果平移后的直線交
,如果平移后的直線交![]() 軸于點
軸于點![]() ,交x軸于點
,交x軸于點![]() ,請確定直線
,請確定直線![]() 的解析式.
的解析式.
(2)如圖2,連接![]() ,求
,求![]() 的長.
的長.
(3)已知點![]() 是直線
是直線![]() 上一個動點,以
上一個動點,以![]() 為對角線的四邊形
為對角線的四邊形![]() 是平行四邊形,當
是平行四邊形,當![]() 取最小值時,請在圖3中畫出滿足條件的
取最小值時,請在圖3中畫出滿足條件的![]() ,并直接寫出此時
,并直接寫出此時![]() 點坐標.
點坐標.
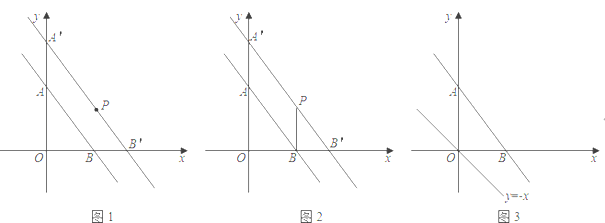
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,矩形
中,矩形![]() 的頂點
的頂點![]() 、
、![]() 在坐標軸上,點
在坐標軸上,點![]() 的坐標為
的坐標為![]() 點
點![]() 從點
從點![]() 出發,在折線段
出發,在折線段![]() 上以每秒3個單位長度向終點
上以每秒3個單位長度向終點![]() 勻速運動,點
勻速運動,點![]() 從點
從點![]() 出發,在折線段
出發,在折線段![]() 上以每秒4個單位長度向終點
上以每秒4個單位長度向終點![]() 勻速運動.兩點同時出發,當其中一個點到達終點時,另一個點也停止運動,連接
勻速運動.兩點同時出發,當其中一個點到達終點時,另一個點也停止運動,連接![]() .設兩點的運動時間為
.設兩點的運動時間為![]() ,線段
,線段![]() 的長度的平方為
的長度的平方為![]() ,即
,即![]() (單位長度2).
(單位長度2).
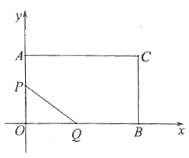
(1)當點![]() 運動到點
運動到點![]() 時,
時,![]() __________
__________![]() ,當點
,當點![]() 運動到點
運動到點![]() 時,
時,![]() __________
__________![]() ;
;
(2)求![]() 關于
關于![]() 的函數解析式,并直接寫出自變量
的函數解析式,并直接寫出自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com