
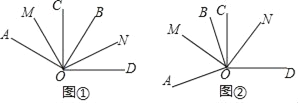
【題目】如圖①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度數;
(2)若(1)中∠BOC=α,其它條件不變,求∠MON的度數;
(3)如圖②,若∠BOC=α,且∠AOD大于平角,其它條件不變,求∠MON的度數.
【答案】(1)∠MON=90°;(2)∠MON=90°;(3)∠MON=90°.
【解析】
(1)由∠AOB=∠COD=90°,∠BOC=20°,可得∠MOC=∠BON的度數,可得∠MON的度數:
(2)同理由∠AOB=∠COD=90°,∠BOC=α,可得∠MOC=∠BON的度數,可得∠MON的度數:
(3)由∠AOB=∠COD=90°,∠BOC=α,可得∠AOC=∠BOD=90°+α,∠MOC=∠BON=45°+![]() α可得∠MON的度數:
α可得∠MON的度數:
解: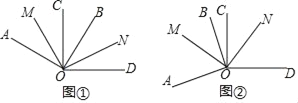
(1)∵∠AOB=∠COD=90°,∠BOC=20°,
∴∠AOC=∠BOD=90°﹣20°=70°.
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠BON=35°,
∴∠MON=∠MOC+∠COB+∠BON=35°+20°+35°=90°;
(2)∵∠AOB=∠COD=90°,∠BOC=α,
∴∠AOC=∠BOD=90°﹣α.
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠BON=45°﹣![]() α,
α,
∴∠MON=∠MOC+∠COB+∠BON=45°﹣![]() α+α+45°﹣
α+α+45°﹣![]() =90°;
=90°;
(3)∵∠AOB=∠COD=90°,∠BOC=α,
∴∠AOC=∠BOD=90°+α.
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=∠BON=45°+![]() α,
α,
∴∠MON=∠MOC﹣∠COB+∠BON=45°+![]() α﹣α+45°+
α﹣α+45°+![]() =90°.
=90°.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
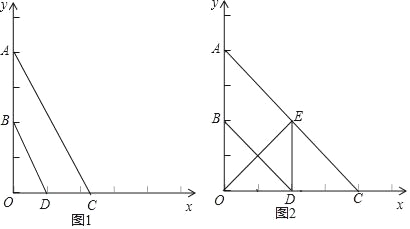
【題目】已知:如圖,平面直角坐標系中,A(0,4),B(0,2),點C是x軸上一點,點D為OC的中點.
(1)求證:BD∥AC;
(2)若點C在x軸正半軸上,且BD與AC的距離等于1,求點C的坐標;
(3)如果OE⊥AC于點E,當四邊形ABDE為平行四邊形時,求直線AC的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次社會調查活動中,小華收集到某“健步走運動”團隊中20名成員一天行走的步數,記錄如下: 5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
對這20個數據按組距1000進行分組,并統計整理,繪制了如下尚不完整的統計圖表: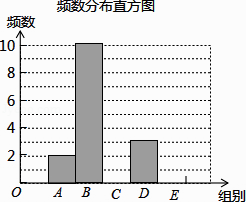
步數分組統計表
組別 | 步數分組 | 頻數 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
請根據以上信息解答下列問題:
(1)求m,n的值;
(2)補全頻數發布直方圖;
(3)這20名“健步走運動”團隊成員一天行走步數的中位數落在哪一組?
(4)若該團隊共有120人,請估計其中一天行走步數不少于7500步的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小玲和小明值日打掃教室衛生,小玲單獨打掃雪20min完成,小明單獨打掃雪16min完成.因小明要將數學作業本交到老師辦公室推遲一會兒,故先由小玲單獨打掃4min,余下的再由兩人一起完成,則兩人一起打掃完教師衛生需要多長時間?設兩人一起打掃完教室衛生需要x min,則根據題意可列方程( )
A. ![]() (x+4)+
(x+4)+![]() x=1 B.
x=1 B. ![]() x+
x+![]() (x+4)=1
(x+4)=1
C. ![]() (x﹣4)+
(x﹣4)+![]() x=1 D.
x=1 D. ![]() x+
x+![]() (x﹣4)=1
(x﹣4)=1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著“互聯網+”時代的到來,一種新型打車方式受到大眾歡迎.該打車方式的計價規則如圖①所示,若車輛以平均速度vkm/h行駛了skm,則打車費用為(ps+60q·![]() )元(不足9元按9元計價).小明某天用該打車方式出行,按上述計價規則,其打車費用y(元)與行駛里程x(km)的函數關系也可由如圖②表示.
)元(不足9元按9元計價).小明某天用該打車方式出行,按上述計價規則,其打車費用y(元)與行駛里程x(km)的函數關系也可由如圖②表示.
(1)當x≥6時,求y與x的函數關系式.
(2)若p=1,q=0.5,求該車行駛的平均速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形![]() 的頂點
的頂點![]() 與坐標原點重合,點
與坐標原點重合,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸的負半軸上,點
軸的負半軸上,點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,一次函數
,一次函數![]() 的圖象過點
的圖象過點![]() 和
和![]() ,反比例函數
,反比例函數![]() 的圖象經過點
的圖象經過點![]() ,且與
,且與![]() 的交點為
的交點為![]() .
.
(1)直接寫出反比例函數解析式 一次函數的解析式 ;
(2)若點![]() 在直線
在直線![]() 上,且使△OPM的面積與四邊形
上,且使△OPM的面積與四邊形![]() 的面積相等,求點
的面積相等,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列兩材料,并解決相關的問題.
(材料一)按照一定順序排列著的一列數稱為數列,排在第一位的數稱為第1項,記為![]() ,依此類推,排在第
,依此類推,排在第![]() 位的數稱為第
位的數稱為第![]() 項,記為
項,記為![]() .一般地,若果一個數列從第二項起,每一項與它前一項的比等于同一個常數,那么這個數列叫作等比數列,這個常數叫作等比數列的公比,公比通常用字母
.一般地,若果一個數列從第二項起,每一項與它前一項的比等于同一個常數,那么這個數列叫作等比數列,這個常數叫作等比數列的公比,公比通常用字母![]() 表示
表示![]() ,如數列
,如數列![]() 為等比數列,其中
為等比數列,其中![]() ,公比
,公比![]() .
.
(材料二)為了求![]() 的值.可令
的值.可令![]()
則![]() , 因此
, 因此![]() ,所以
,所以![]() ,
,
即![]()
(1)等比數列![]() 的公比
的公比![]() 為_________,第6項是________
為_________,第6項是________
(2)如果一個數列![]() 是等比數列,且公比為
是等比數列,且公比為![]() ,那么根據定義可得到
,那么根據定義可得到![]() ,
,![]() ,
,![]() ,由此可得
,由此可得![]() (用
(用![]() 和
和![]() 的代數式表示)
的代數式表示)
(3)若某等比數列的公比![]() ,第2項
,第2項![]() ,則它的第1項
,則它的第1項![]() ,第4項
,第4項![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣ ![]() x2+mx+n與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).
x2+mx+n與x軸交于A、B兩點,與y軸交于點C,拋物線的對稱軸交x軸于點D,已知A(﹣1,0),C(0,2).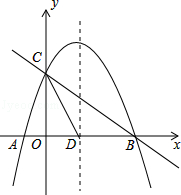
(1)求拋物線的表達式;
(2)在拋物線的對稱軸上是否存在點P,使△PCD是以CD為腰的等腰三角形?如果存在,直接寫出P點的坐標;如果不存在,請說明理由;
(3)點E是線段BC上的一個動點,過點E作x軸的垂線與拋物線相交于點F,當點E運動到什么位置時,四邊形CDBF的面積最大?求出四邊形CDBF的最大面積及此時E點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com