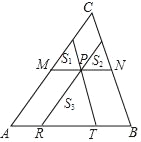
【題目】如圖，已知P為△ABC內一點，過P點分別作直線平行于△ABC的各邊，形成小三角形的面積S1、S2、S3，分別為4、9、49，則△ABC的面積為_____．
口算題卡加應用題集訓系列答案科目：初中數學 來源： 題型：
【題目】認真閱讀下面的材料，完成有關問題：
材料：在學習絕對值時，我們已了解絕對值的幾何意義，如|5-3|表示5、3在數軸上對應的兩點之間的距離；又如|5+3|=|5-（-3）|，所以|5+3|表示5、-3在數軸上對應的兩點之間的距離。因此，一般地，點A,B在數軸上分別表示有理數a,b，那么A,B之間的距離（也就是線段AB的長度）可表示為|a-b|。
因此我們可以用絕對值的幾何意義按如下方法求
的最小值；
即數軸上x與1對應的點之間的距離，
即數軸上x與2對應的點之間的距離，把這兩個距離在同一個數軸上表示出來，然后把距離相加即可得原式的值.
設A、B、P三點對應的數分別是1、2、x.
當1≤x≤2時，即P點在線段AB上，此時
；
當x＞2時，即P點在B點右側，此時＝ PA＋PB＝AB＋2PB＞AB；
當x ＜1時，即P點在A點左側，此時＝PA＋PB＝AB＋2PA＞AB；
綜上可知，當1≤x≤2時（P點在線段AB上），取得最小值為1．
請你用上面的思考方法結合數軸完成以下問題：
（1）滿足
的x的取值范圍是 。
（2）求
的最小值為 ，最大值為 。
備用圖：
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，△ABC的位置如圖所示（每個小方格都是邊長為1個單位長度的正方形）．
（1）將△ABC沿x軸方向向左平移6個單位，畫出平移后得到的△A1B1C1；
（2）將△ABC繞著點A順時針旋轉90°，畫出旋轉后得到的△AB2C2，并直接寫出點B2、C2的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀以下材料，完成下列問題.
（1）我們已經學過了乘方運算，我們知道表示2個-2相乘，即
，那么
表示 ，把
寫成乘方的形式表示為 ，此時底數是 .
（2）將（1）中兩個底數同為-2的冪相乘，即
，結果共有 個-2相乘，寫成冪的形式為 ；
（3）若將（2）中算式中的底數都換為
，則
表示 ，計算結果為 .
若將（2）中算式中的指數換為正整數
，則
，請用一句話概括你發現的結論 ；
（4）利用上述結論，完成以下填空
若
，則
，
；
若
，
，
，寫出
的數量關系 .
查看答案和解析>>
科目：初中數學 來源： 題型：
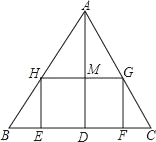
【題目】如圖，△ABC是一張銳角三角形的硬紙片．AD是邊BC上的高，BC=40cm，AD=30cm．從這張硬紙片剪下一個長HG是寬HE的2倍的矩形EFGH．使它的一邊EF在BC上，頂點G，H分別在AC，AB上．AD與HG的交點為M．
（1）求證： 
；
（2）求這個矩形EFGH的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，O為坐標原點，已知直線
經過點A（-6,0），它與y軸交于點B,點B在y軸正半軸上，且OA=2OB
（1）求直線的函數解析式
（2）若直線
也經過點A（-6,0），且與y軸交于點C，如果ΔABC的面積為6，求C點的坐標
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，ABCD中，E，F是對角線BD上的兩點，如果添加一個條件，使△ABE≌△CDF，則添加的條件不能為（ ）
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 
一定是一次函數
B. 有的實數在數軸上找不到對應的點
C. 長為
的三條線段能組成直角三角形
D. 無論
為何值，點
總是在第二象限
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
