
【題目】如圖,在邊長為4的正方形ABCD中,P是BC邊上一動點(不含B、C兩點),將 ![]() ABP沿直線AP翻折,點B落在點E處;在CD上有一點M,使得將
ABP沿直線AP翻折,點B落在點E處;在CD上有一點M,使得將 ![]() CMP沿直線MP翻折后,點C落在直線PE上的點F處,直線PE交CD于點N,連接MA,NA.則以下結論中正確的個數有( ).
CMP沿直線MP翻折后,點C落在直線PE上的點F處,直線PE交CD于點N,連接MA,NA.則以下結論中正確的個數有( ).
① ![]() CMP∽
CMP∽ ![]() BPA;
BPA;
②四邊形AMCB的面積最大值為10;
③當P為BC中點時,AE為線段NP的中垂線;
④線段AM的最小值為2 ![]() ;
;
⑤當 ![]() ABP≌
ABP≌ ![]() AND時,BP=4
AND時,BP=4 ![]() -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
【答案】D
【解析】解: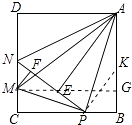 ∵∠APB=∠APE,∠MPC=∠MPN,
∵∠APB=∠APE,∠MPC=∠MPN,
∵∠CPN+∠NPB=180°,
∴2∠NPM+2∠APE=180°,
∴∠MPN+∠APE=90°,
∴∠APM=90°,
∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,
∴∠CPM=∠PAB,
∵四邊形ABCD是正方形,
∴AB=CB=DC=AD=4,∠C=∠B=90°,
∴△CMP∽△BPA.故①正確,
設PB=x,則CP=4-x,
∵△CMP∽△BPA,
∴![]() =
=![]() ,
,
∴CM=![]() x(4-x),
x(4-x),
∴S四邊形AMCB=![]() [4+
[4+![]() x(4-x)]×4=-
x(4-x)]×4=-![]() x2+2x+8=-
x2+2x+8=-![]() (x-2)2+10,
(x-2)2+10,
∴x=2時,四邊形AMCB面積最大值為10,故②正確,
易證得△ADN≌△AEN,當PB=PC=PE=2時,設ND=NE=y,
在RT△PCN中,(y+2)2=(4-y)2+22解得y=![]() ,
,
∴NE≠EP,故③錯誤,
作MG⊥AB于G,
∵AM=![]() =
=![]() ,
,
∴AG最小時AM最小,
∵AG=AB-BG=AB-CM=4-![]() x(4-x)=
x(4-x)=![]() (x-2)2+3,
(x-2)2+3,
∴x=2時,AG最小值=3,
∴AM的最小值=![]() =5,故④錯誤.
=5,故④錯誤.
∵△ABP≌△ADN時,
∴∠PAB=∠DAN=22.5°,在AB上取一點K使得AK=PK,設PB=z,
∴∠KPA=∠KAP=22.5°
∵∠PKB=∠KPA+∠KAP=45°,
∴∠BPK=∠BKP=45°,
∴PB=BK=z,AK=PK=![]() z,
z,
∴z+![]() z=4,
z=4,
∴z=4![]() -4,
-4,
∴PB=4![]() -4,故⑤正確.
-4,故⑤正確.
故正確的為①②⑤.
故選D.
【考點精析】關于本題考查的相似三角形的判定與性質,需要了解相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖,半圓O的直徑AB=10,有一條定長為6的動弦CD在弧AB上滑動(點C、點D分別不與點A、點B重合),點E、F在AB上,EC⊥CD,FD⊥CD. 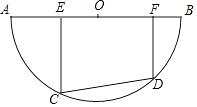
(1)求證:EO=OF;
(2)聯結OC,如果△ECO中有一個內角等于45°,求線段EF的長;
(3)當動弦CD在弧AB上滑動時,設變量CE=x,四邊形CDFE面積為S,周長為l,問:S與l是否分別隨著x的變化而變化?試用所學的函數知識直接寫出它們的函數解析式及函數定義域,以說明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我省某工藝廠為全運會設計了一款成本為每件20元的工藝品,投放市場試銷后發現每天的銷售量y(件)是售價x(元/件)的一次函數。當售價為22元/件時,每天銷售量為780件;當售價為25元/件時,每天銷售量為750件。
(1)求y與x的函數關系式;
(2)如果該工藝品售價最高不超過每件30元,那么售價定為每件多少元時,工藝廠銷售該工藝品每天獲得的利潤最大?最大利潤是多少元?(利潤=售價-成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下列一段文字,再回答后面的問題.
已知在平面內兩點P1(x1,y1),P2(x2,y2),這兩點間的距離P1P2=![]() ,同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可簡化為|x2﹣x1|或|y2﹣y1|.
,同時,當兩點所在的直線在坐標軸或平行于坐標軸或垂直于坐標軸時,兩點間距離公式可簡化為|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,3),B(﹣2,﹣1),試求A,B兩點間的距離;
(2)已知A,B在平行于y軸的直線上,點A的縱坐標為7,點B的縱坐標為﹣2,試求A,B兩點間的距離;
(3)已知一個三角形各頂點坐標為A(0,5),B(﹣3,2),C(3,2),你能判斷此三角形的形狀嗎?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P1、P2是反比例函數y= ![]() (k>0)在第一象限圖象上的兩點,點A1的坐標為(4,0).若△P1OA1與△P2A1A2均為等腰直角三角形,其中點P1、P2為直角頂點.
(k>0)在第一象限圖象上的兩點,點A1的坐標為(4,0).若△P1OA1與△P2A1A2均為等腰直角三角形,其中點P1、P2為直角頂點. 
(1)求反比例函數的解析式.
(2)①求P2的坐標. ②根據圖象直接寫出在第一象限內當x滿足什么條件時,經過點P1、P2的一次函數的函數值大于反比例函數y= ![]() 的函數值.
的函數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)在直角坐標系中,先描出點A(1,3),點B(4,1).并直接寫出點A關于x軸的對稱的A1的坐標A1 ( , ).
(2)在x軸上找一點C,使AC+BC的值最小; (保留作圖痕跡).
(3)用尺規在x軸上找一點P,使PA=PB(保留作圖痕跡).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某產品每件成本10元,試銷階段每件產品的銷售單價x(元/件)與日銷售量y(件)之間的關系如下表.
x(元∕件) | 15 | 18 | 20 | 22 | … |
y(件) | 250 | 220 | 200 | 180 | … |
按照這樣的規律可得,日銷售利潤w(元)與銷售單價x(元/件)之間的函數關系式是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com