
【題目】如圖1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏將一塊三角板中含45°角的頂點放在A上,從AB邊開始繞點A逆時針旋轉一個角α,其中三角板斜邊所在的直線交直線BC于點D,直角邊所在的直線交直線BC于點E.
(1)小敏在線段BC上取一點M,連接AM,旋轉中發現:若AD平分∠BAM,則AE也平分∠MAC.請你證明小敏發現的結論;
(2)當0°<α≤45°時,小敏在旋轉中還發現線段BD、CE、DE之間存在如下等量關系:BD2+CE2=DE2.同組的小穎和小亮隨后想出了相同的方法進行解決:將△ABD沿AD所在的直線對折得到△ADF(如圖2);請證明小敏的發現的是正確的.

【答案】見解析
【解析】試題分析:(1)如圖1,根據圖形、已知條件推知∠BAD+∠MAE=∠DAM+∠EAC=45°,所以∠MAE=∠EAC,即AE平分∠MAC;(2)小穎的方法是應用折疊對稱的性質和SAS得到△AEF≌△AEC,在Rt△OCE中應用勾股定理而證明;小亮的方法是將△ABD繞點A逆時針旋轉90°得到△ACG,根據旋轉的性質用SAS得到△ACE≌△ACG,從而在Rt△CEG中應用勾股定理而證明.
試題解析:1)證明:如圖1,∵∠BAC=90°,
∴∠BAD+∠DAM+∠MAE+∠EAC=90°.
∵∠DAE=45°,
∴∠BAD+∠EAC=45°.
∵∠BAD=∠DAM,
∴∠BAD+∠EAC=∠DAM+∠EAC=45°,
∴∠BAD+∠MAE=∠DAM+∠EAC,
∴∠MAE=∠EAC,即AE平分∠MAC;
(2)如圖2,連接EF.

由折疊可知,∠BAD=∠FAD,AB=AF,BD=DF,
∵∠BAD=∠FAD,
∴由(1)可知,∠CAE=∠FAE.
在△AEF和△AEC中,
∵ AF=AC,∠FAE=∠CAE,AE=AE ,
∴△AEF≌△AEC(SAS),
∴CE=FE,∠AFE=∠C=45°.
∴∠DFE=∠AFD+∠AFE=90°.
在Rt△DFE中,DF2+FE2=DE2,
∴BD2+CE2=DE2. (利用旋轉的方法證明相應給分)


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:
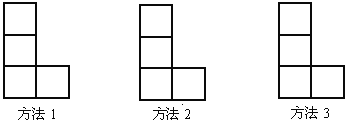
【題目】① 如圖,由小正方形組成的L形圖中,用三種方法分別在圖中添一個小正方形使圖形成為軸對稱圖形:
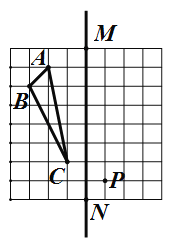
② 如圖,在正方形網格上的一個△ABC.
⑴ 作△ABC關于直線MN的對稱圖形(不寫作法);
⑵ 以P為一個頂點作與△ABC全等的三角形(規定點P與點B對應,另兩頂點都在圖中網格交點處),則可作出 個三角形與△ABC全等.
查看答案和解析>>
科目:初中數學 來源: 題型:
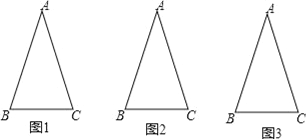
【題目】如圖,△ABC中,AB=AC,∠A=36°,稱滿足此條件的三角形為黃金等腰三角形.請完成以下操作:(畫圖不要求使用圓規,以下問題所指的等腰三角形個數均不包括△ABC)
(1)在圖1中畫1條線段,使圖中有2個等腰三角形,并直接寫出這2個等腰三角形的頂角度數分別是 度和 度;
(2)在圖2中畫2條線段,使圖中有4個等腰三角形;
(3)繼續按以上操作發現:在△ABC中畫n條線段,則圖中有 個等腰三角形,其中有 個黃金等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
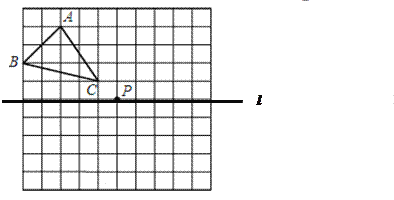
【題目】如圖,一個10×10網格,每個小正方形的邊長均為1,每個小正方形的頂點叫格點,△ABC的頂點均在格點上.
(1)畫出△ABC關于直線l的對稱的△A1B1C1.
(2)畫出△ABC關于點P的中心對稱圖形△A2B2C2.
(3)△A1B1C1與△A2B2C2組成的圖形_______________(是或否)軸對稱圖形,如果是軸對稱圖形,請畫出對稱軸.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com