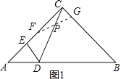
【題目】如圖，在
中
，
，點
在
邊上，
于點
．
若
，
，求
的長；
設點
在線段上，點
在射線
上，以，
，為頂點的三角形與
有一個銳角相等，
交
于點
．問：線段
可能是
的高線還是中線？或兩者都有可能？請說明理由．
【答案】（1）6；（2）見解析
【解析】
（1）根據已知條件易證DE∥BC，再由平行線分線段成比例定理列比例式即可求解；（2）分三種情況討論：①若∠CFG=∠ECD，此時線段CP是△CFG的FG邊上的中線；②若∠CFG=∠EDC，此時線段CP為△CFG的FG邊上的高線；③當CD為∠ACB的平分線時，CP既是△CFG的FG邊上的高線又是中線．
解：
∵
，
，
∴
，
∴
，
∵
，
，
∴
；
①如圖
，若
，此時線段
是
的
邊上的中線．
證明：∵
，
，
又∵，
∴
，
∴
，
∵，
∴
，
∴
，
∴線段是的邊上的中線；
②如圖
，若
，此時線段為的邊上的高線．
證明：∵，
∴
，
∵，
∴
，
∴
，
∴線段為的邊上的高線．
③如圖
，當
為
的平分線時，既是的邊上的高線又是中線．
科目：初中數學 來源： 題型：
【題目】我們知道，有理數包括整數、有限小數和無限循環小數，事實上，所有的有理數都可以化為分數形式（整數可看作分母為1的分數），那么無限循環小數如何表示為分數形式呢？請看以下示例：
例：將
化為分數形式
由于=0.777…，設x=0.777…①
則10x=7.777…②
②﹣①得9x=7，解得x=
，于是得=．
同理可得
=
，
=1+
=1+
，
根據以上閱讀，回答下列問題：（以下計算結果均用最簡分數表示）
（基礎訓練）
（1）
= ，
= ；
（2）將
化為分數形式，寫出推導過程；
（能力提升）
（3）
= ，
= ；
（注：=0.315315…，=2.01818…）
（探索發現）
（4）①試比較
與1的大小： 1（填“＞”、“＜”或“=”）
②若已知
=
，則
= ．
（注：=0.285714285714…）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解：在平面直角坐標系xOy中，對于任意兩點P1（x1，y1）與P2（x2，y2）的“非常距離”，給出如下定義：
若|x1﹣x2|≥|y1﹣y2|，則點P1與點P2的“非常距離”為|x1﹣x2|；
若|x1﹣x2|＜|y1﹣y2|，則點P1與點P2的“非常距離”為|y1﹣y2|．
例如：點P1（1，1），點P2（2，3），因為|1﹣2|＜|1﹣3|，所以點P1與點P2的“非常距離”為|1﹣3|＝2，也就是圖1中線段P1Q與線段P2Q長度的較大值（點Q為垂直于y軸的直線P1Q與垂直于x軸的直線P2Q的交點）．
（1）已知點A（-
，0），B為y軸上的一個動點．
①若點B（0，3），則點A與點B的“非常距離”為______；
②若點A與點B的“非常距離”為2，則點B的坐標為_______；
③直接寫出點A與點B的“非常距離”的最小值為_______；
（2）已知點D（0，1），點C是直線y＝﹣
x+3上的一個動點，如圖2，求點C與點D“非常距離”的最小值及相應的點C的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：四邊形ABCD的對角線AC，BD相交于點O，給出下列4個條件：①AB∥CD；②OA＝OC；③AB＝CD；④AD∥BC.從中任取兩個條件，能推出四邊形ABCD是平行四邊形的概率是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠C=90°,AE平分∠BAC交BC于點E,O是AB上一點，經過A,E兩點的⊙O交AB于點D，連接DE，作∠DEA的平分線EF交⊙O于點F，連接AF.
（1）求證：BC是⊙O的切線；
（2）若sin∠EFA=
,AF=
,求線段AC的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面的材料，回答問題：
解方程
，這是一個一元四次方程，根據該方程的特點，它的解法通常是：
設
，那么
，于是原方程可變為
①，解得
，
．
當
時，
，∴
；
當
時，
，∴
；
∴原方程有四個根：
，
，
，
．
在由原方程得到方程①的過程中，利用________法達到________的目的，體現了數學的轉化思想．
解方程
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
