
【題目】如圖,y軸上有一點A(0,1),點B是x軸上一點,∠ABO=60°,拋物線y=﹣![]() x2+
x2+![]() +3
+3![]() 與x軸交于C、D兩點(點C在點D的左側).
與x軸交于C、D兩點(點C在點D的左側).
(1)將點C向右平移![]() 個單位得到點E,過點E作直線l⊥x軸,點P為y軸上一動點,過點P作PQ⊥y軸交直線l于點Q,點K為拋物線上第一象限內的一個動點,當△ABK面積最大時,求KQ+QP+PE的最小值,及此時點P的坐標;
個單位得到點E,過點E作直線l⊥x軸,點P為y軸上一動點,過點P作PQ⊥y軸交直線l于點Q,點K為拋物線上第一象限內的一個動點,當△ABK面積最大時,求KQ+QP+PE的最小值,及此時點P的坐標;
(2)在(1)的條件下,將線段PE繞點P逆時針旋轉90°后得線段PE′,問:在第一象限內是否存在點S,使得△SPE'是有一個角為60°,且以線段PE′為斜邊的直角三角形,若存在請直接寫出所有滿足條件的點S,若不存在,請說明理由.

【答案】(1)7,(0,![]() );(2)存在,S2(
);(2)存在,S2(![]() ,
,![]() ),S3(
),S3(![]() ,
,![]() ),S4(
),S4(![]() ,
,![]() )
)
【解析】
(1)解直角三角形求出OB,求出直線AB的解析式,構建方程組轉化為一元二次方程,利用△=0,確定點K的坐標,如圖1中,點K向右平移一個單位得到K′(2,3![]() ),連接K′E,則KQ+QP+PE的最小值=K′E+QP,再求出EK′的解析式即可求出點P的坐標.
),連接K′E,則KQ+QP+PE的最小值=K′E+QP,再求出EK′的解析式即可求出點P的坐標.
(2)由(1)可知E(﹣1,0),P(0,![]() ),將PE繞點P逆時針旋轉90°得到PE′,可得E′(
),將PE繞點P逆時針旋轉90°得到PE′,可得E′(![]() ,
,![]() ﹣1),以PE′為邊作等邊三角形PE′N,等邊三角形PE′M,可得M(0,
﹣1),以PE′為邊作等邊三角形PE′N,等邊三角形PE′M,可得M(0,![]() ﹣2),N(
﹣2),N(![]() ,
,![]() +1),此時四邊形PME′N是菱形,取各邊的中點S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′為斜邊的直角三角形,再根據點S在第一象限,即可解決問題.
+1),此時四邊形PME′N是菱形,取各邊的中點S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′為斜邊的直角三角形,再根據點S在第一象限,即可解決問題.
解:(1)由題意在Rt△AOB中,∵OA=1,∠ABO=60°,
∴BO=![]() OA=
OA=![]() ,
,
∴B(![]() ,0),
,0),
設直線AB的解析式為y=kx+b,把A(0,1),B(![]() ,0)代入可得
,0)代入可得
 ,解得
,解得 ,
,
∴直線AB的解析式為y=﹣![]() x+1,
x+1,
對于拋物線y=﹣![]() x2+
x2+![]() x+3
x+3![]() ,令y=0,得到x2﹣x﹣3=0,解得x=
,令y=0,得到x2﹣x﹣3=0,解得x=![]() ,
,
則C(![]() ,0),D(
,0),D(![]() ,0),
,0),
將點C向右平移![]() 個單位得到E(﹣1,0),
個單位得到E(﹣1,0),
設平行于AB的解析式為y=﹣![]() x+m,
x+m,
由 ,
,
消去y得到﹣![]() x2+2
x2+2![]() x+3
x+3![]() ﹣m=0,
﹣m=0,
由△=0得到m=﹣4![]() ,xk=﹣1,yk=3
,xk=﹣1,yk=3![]() ,
,
則K(1,3![]() ),
),
如圖1中,點K向右平移一個單位得到K′(2,3![]() ),連接K′E,
),連接K′E,

則KQ+QP+PE的最小值=K′E+QP=![]() ,
,
∵E(﹣1,0),K′(2,3![]() ),
),
∴直線EK′的解析式為y=![]() x+
x+![]() ,
,
∴P(0,![]() ).
).
(2)如圖2中,

由(1)可知E(﹣1,0),P(0,![]() ),將PE繞點P逆時針旋轉90°得到PE′,可得E′(
),將PE繞點P逆時針旋轉90°得到PE′,可得E′(![]() ,
,![]() ﹣1),
﹣1),
以PE′為邊作等邊三角形PE′N,等邊三角形PE′M,
可得M(0,![]() ﹣2),N(
﹣2),N(![]() ,
,![]() +1),此時四邊形PME′N是菱形,取各邊的中點S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′為斜邊的直角三角形,
+1),此時四邊形PME′N是菱形,取各邊的中點S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′為斜邊的直角三角形,
∵點S在第一象限,
∴滿足條件的點S2(![]() ,
,![]() ),S3(
),S3(![]() ,
,![]() ),S4(
),S4(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D、E是BC邊上的點,BD:DE:EC=3:2:1,M在AC邊上,CM:MA=1:2,BM交AD,AE于H,G,則BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABD中,C為BD上一點,使得CA=CD,過點C作CE∥AD交AB于點E,過點D作DF⊥AD交AC的處長線于點F.
(1)若CD=3,求AF的長;
(2)若∠B=30°,∠ADC=40°,求證:AC=EC.

查看答案和解析>>
科目:初中數學 來源: 題型:
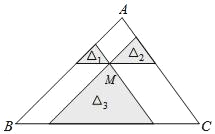
【題目】如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1、△2、△3(圖中陰影部分)的面積分別是1、4、25.則△ABC的面積是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,已知點A(2,2),B(4,0).若在坐標軸上取點C,使△ABC為等腰三角形,則滿足條件的點C的個數是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于點M,連接CM.
(1)求證:BE=AD;并用含α的式子表示∠AMB的度數;
(2)當α=90°時,取AD,BE的中點分別為點P、Q,連接CP,CQ,PQ,如圖2,判斷△CPQ的形狀,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初三年級261位學生參加期末考試,某班35位學生的語文成績、數學成績與總成績在全年級中排名情況如圖1和圖2所示,甲、乙、丙為該班三位學生.

從這次考試成績看,①在甲、乙兩人中,總成績名次靠前的學生是______;
②在語文和數學兩個科目中,丙同學的成績名次更靠前的科目是______.
你選擇的理由是____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】1979年,在鄧小平同志的提議下,第五屆全國人大常委會第六次會議決定每年3月12日為我國的植樹節,今年是第40個植樹節,明德中學師生積極響應國家“綠水青山就是金山銀山”的號召,到距學校20千米的山上義務植樹,老師和男生騎自行車先走,走了16千米后,女生乘汽車拉著工具、樹苗出發,結果同時到達.已知汽車的速度比自行車的速度快60千米/小時,求兩種車的速度各是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com