
【題目】如圖,矩形ABCD中,∠ACB=30°,將一塊直角三角板的直角頂點P放在兩對角線AC,BD的交點處,以點P為旋轉中心轉動三角板,并保證三角板的兩直角邊分別于邊AB,BC所在的直線相交,交點分別為E,F.
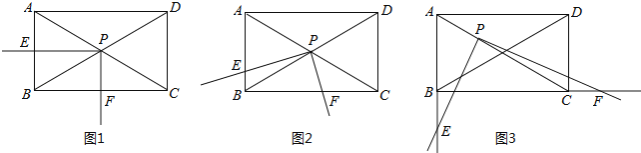
(1)當PE⊥AB,PF⊥BC時,如圖1,則![]() 的值為 ;
的值為 ;
(2)現將三角板繞點P逆時針旋轉α(0°<α<60°)角,如圖2,求![]() 的值;
的值;
(3)在(2)的基礎上繼續旋轉,當60°<α<90°,且使AP:PC=1:2時,如圖3,![]() 的值是否變化?證明你的結論.
的值是否變化?證明你的結論.
【答案】解:(1)![]() 。
。
(2)如答圖1,過點P作PM⊥AB于點M,PN⊥BC于點N,則PM⊥PN。
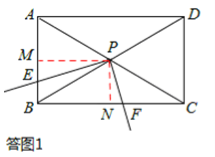
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
由(1)知,![]() ,
,
∴![]() 。
。
(3)變化。證明如下:
如答圖2,過點P作PM⊥AB于點M,PN⊥BC于點N,則PM⊥PN,PM∥BC,PN∥AB。
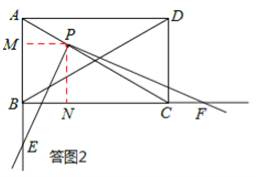
∵PM∥BC,PN∥AB,
∴∠APM=∠PCN,∠PAM=∠CPN。
∴△APM∽△PCN。
∴![]() ,得CN=2PM。
,得CN=2PM。
在Rt△PCN中,![]() ,
,
∴![]() 。
。
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
∴![]() 的值發生變化
的值發生變化
【解析】
試題(1)證明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得![]() 的值:
的值:
∵矩形ABCD,∴AB⊥BC,PA=PC。
∵PE⊥AB,BC⊥AB,∴PE∥BC。∴∠APE=∠PCF。
∵PF⊥BC,AB⊥BC,∴PF∥AB。∴∠PAE=∠CPF。
∵在△APE與△PCF中,∠PAE=∠CPF,PA=PC,∠APE=∠PCF,
∴△APE≌△PCF(ASA)。∴PE=CF。
在Rt△PCF中,![]() ,∴
,∴![]() 。
。
(2)如答圖1所示,作輔助線,構造直角三角形,證明△PME∽△PNF,并利用(1)的結論,求得![]() 的值;
的值;
(3)如答圖2所示,作輔助線,構造直角三角形,首先證明△APM∽△PCN,求得![]() ;然后證明△PME∽△PNF,從而由
;然后證明△PME∽△PNF,從而由![]() 求得
求得![]() 的值。與(1)(2)問相比較,
的值。與(1)(2)問相比較,![]() 的值發生了變化。
的值發生了變化。


科目:初中數學 來源: 題型:
【題目】用1塊![]() 型鋼板可制成2塊
型鋼板可制成2塊![]() 型鋼板和1塊
型鋼板和1塊![]() 型鋼板;用1塊
型鋼板;用1塊![]() 型鋼板可制成1塊
型鋼板可制成1塊![]() 型鋼板和3塊
型鋼板和3塊![]() 型鋼板.現準備購買
型鋼板.現準備購買![]() 、
、![]() 型鋼板共100塊,并全部加工成
型鋼板共100塊,并全部加工成![]() 、
、![]() 型鋼板.要求
型鋼板.要求![]() 型鋼板不少于120塊,
型鋼板不少于120塊,![]() 型鋼板不少于250塊,設購買
型鋼板不少于250塊,設購買![]() 型鋼板
型鋼板![]() 塊(
塊(![]() 為整數)
為整數)
(1)求![]() 、
、![]() 型鋼板的購買方案共有多少種?
型鋼板的購買方案共有多少種?
(2)出售![]() 型鋼板每塊利潤為100元,
型鋼板每塊利潤為100元,![]() 型鋼板每塊利潤為120元.若將
型鋼板每塊利潤為120元.若將![]() 、
、![]() 型鋼板全部出售,請你設計獲利最大的購買方案,并求出最大利潤.
型鋼板全部出售,請你設計獲利最大的購買方案,并求出最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
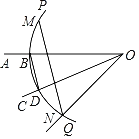
【題目】如圖:已知銳角∠AOC,依次按照以下順序操作畫圖:
(1)在射線OA上取一點B,以點O為圓心,OB長為半徑作![]() ,交射線OC于點D,連接BD;
,交射線OC于點D,連接BD;
(2)分別以點B,D為圓心,BD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接ON,MN.
根據以上作圖過程及所作圖形可知下列結論:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,則MN=![]() ON.其中正確結論的序號是_____.
ON.其中正確結論的序號是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的布袋里裝有4個標有1,2,3,4的小球,它們的形狀、大小、質地完全相同,小李從布袋里隨機取出一個小球,記下數字為x,小張在剩下的3個小球中隨機取出一個小球,記下數字為y,這樣確定了點Q的坐標(x,y).
(1)畫樹狀圖或列表,寫出點Q所有可能的坐標;
(2)求點Q(x,y)在函數y=﹣x+5圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
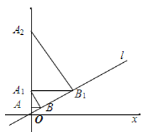
【題目】如圖,已知直線l:y=![]() x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;……按此作法繼續下去,則點A2020的坐標為______________.
x,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2;……按此作法繼續下去,則點A2020的坐標為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將圖中的A型、B型、C型矩形紙片分別放在3個盒子中,盒子的形狀、大小、質地都相同,再將這3個盒子裝入一只不透明的袋子中.
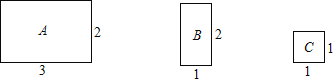
(1)攪勻后從中摸出1個盒子,求摸出的盒子中是![]() 型矩形紙片的概率;
型矩形紙片的概率;
(2)攪勻后先從中摸出1個盒子(不放回),再從余下的兩個盒子中摸出一個盒子,求2次摸出的盒子的紙片能拼成一個新矩形的概率(不重疊無縫隙拼接).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點P為△ABC邊上一動點,沿著A→C→B的路徑行進,點P作PD⊥AB,垂足為D,設AD=x,△APD的面積為y,圖2是y關于x的函數圖象,則依據圖中的數量關系計算△ACB的周長為( )
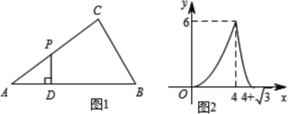

A.![]() B.15C.
B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
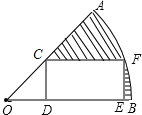
【題目】如圖,在半徑為![]() ,圓心角等于45°的扇形AOB內部作一個矩形CDEF,使點C在OA上,點D、E在OB上,點F在弧AB上,且DE=2CD,則:
,圓心角等于45°的扇形AOB內部作一個矩形CDEF,使點C在OA上,點D、E在OB上,點F在弧AB上,且DE=2CD,則:
(1)弧AB的長是(結果保留π)________;
(2)圖中陰影部分的面積為(結果保留π)________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com