
【題目】在⊙O中,直徑AB=6,BC是弦,∠ABC=30°,點P在BC上,點Q在⊙O上,且OP⊥PQ.
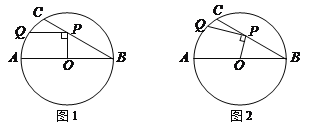
(1)如圖1,當(dāng)PQ∥AB時,求PQ的長度;
(2)如圖2,當(dāng)點P在BC上移動時,求PQ長的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)在Rt△OPB中,由OP=OB·tan∠ABC可求得OP=![]() ,連接OQ,在Rt△OPQ中,根據(jù)勾股定理可得PQ的長;(2)由勾股定理可知
,連接OQ,在Rt△OPQ中,根據(jù)勾股定理可得PQ的長;(2)由勾股定理可知![]() OQ為定值,所以當(dāng)當(dāng)OP最小時,PQ最大.根據(jù)垂線段最短可知,當(dāng)OP⊥BC時OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的長;在Rt△OPQ中,根據(jù)勾股定理求得PQ的長.
OQ為定值,所以當(dāng)當(dāng)OP最小時,PQ最大.根據(jù)垂線段最短可知,當(dāng)OP⊥BC時OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的長;在Rt△OPQ中,根據(jù)勾股定理求得PQ的長.

試題解析:解:(1)∵OP⊥PQ,PQ∥AB,∴OP⊥AB.
在Rt△OPB中,OP=OB·tan∠ABC=3·tan30°=![]() .
.
連接OQ,在Rt△OPQ中, ![]() .
.
(2) ∵![]()
∴當(dāng)OP最小時,PQ最大,此時OP⊥BC.
OP=OB·sin∠ABC=3·sin30°=![]() .
.
∴PQ長的最大值為 .
.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 中,對角線
中,對角線![]() 交于點
交于點![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.下列結(jié)論正確的是( )
的中點.下列結(jié)論正確的是( )
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() ;⑤四邊形
;⑤四邊形![]() 是菱形.
是菱形.
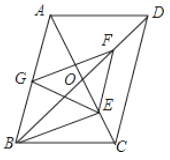
A.③⑤B.①②④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
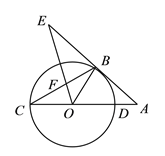
【題目】如圖, ![]() 為⊙
為⊙![]() 的直徑,點
的直徑,點![]() 在⊙
在⊙![]() 上,連接
上,連接![]() 、
、![]() ,過點
,過點![]() 的切線
的切線![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,
, ![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
(![]() )求證:
)求證: ![]() .
.
(![]() )若⊙
)若⊙![]() 的半徑為
的半徑為![]() ,
, ![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一個不透明的袋子中裝有僅顏色不同的10個小球,其中紅球4個,黑球6個.
(1)先從袋子中取出m(m>1)個紅球,再從袋子中隨機(jī)摸出1個球,將“摸出黑球”記為事件A,請完成下列表格;
![]()
(2)先從袋子中取出m個紅球,再放入m個一樣的黑球并搖勻,隨機(jī)摸出1個黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
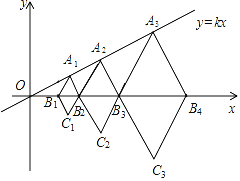
【題目】含60°角的菱形A1B1C1B2,A2B2C2B3,A3B3C3B4,…,按如圖的方式放置在平面直角坐標(biāo)系xOy中,點A1,A2,A3,…,和點B1,B2,B3,B4,…,分別在直線y=kx和x軸上.已知B1(2,0),B2(4,0),則點A1的坐標(biāo)是_____;點A3的坐標(biāo)是_____;點An的坐標(biāo)是____(n為正整數(shù)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商店經(jīng)銷一種成本為每千克40元的水產(chǎn)品,據(jù)市場分析,若按每千克50元銷售,一個月能售出500千克.若銷售價每漲1元,則月銷售量減少10千克.
(1)要使月銷售利潤達(dá)到最大,銷售單價應(yīng)定為多少元?
(2)要使月銷售利潤不低于8000元,請結(jié)合圖象說明銷售單價應(yīng)如何定?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=80°,AB的垂直平分線交對角線AC于點F,垂足為E,連接DF,則∠CDF等于()

A.50°B.60°C.70°D.80°
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com