
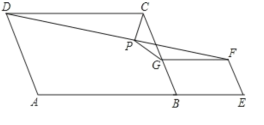
【題目】如圖,在平行四邊形ABCD和平行四邊形BEFG中,AB=AD,BG=BE,點A、 B、 E在同一直線上,P是線段DF的中點,連接PG、PC,若∠ABC=∠BEF=60°,則![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
可通過構建全等三角形求解.延長GP交DC于H,可證三角形DHP和PGF全等,已知的有DC∥GF,根據平行線間的內錯角相等可得出兩三角形中兩組對應的角相等,又有DP=PF,因此構成了全等三角形判定條件中的(AAS),于是兩三角形全等,那么HP=PG,可根據三角函數來得出PG、CP的比例關系.
延長GP交DC于點H,
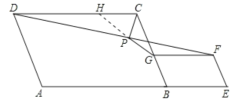
∵AB=AD,BG=BE,
∴平行四邊形ABCD和平行四邊形BEFG都是菱形,
∵P是線段DF的中點,
∴FP=DP,
由題意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GP=HP,GF=HD,
∵四邊形ABCD是菱形,
∴CD=CB,
∴CG=CH
∴△CHG是等腰三角形,
∴PG⊥PC,(三線合一)
又∵∠ABC=∠BEF=60°,
∴∠GCP=60°,
∴![]() =
=![]() .
.
故選B.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案 沖刺100分單元優(yōu)化練考卷系列答案
沖刺100分單元優(yōu)化練考卷系列答案科目:初中數學 來源: 題型:
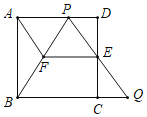
【題目】如圖,在邊長為l的正方形ABCD中,E是邊CD的中點,點P是邊AD上一點(與點A、D不重合),射線PE與BC的延長線交于點Q.
(1)求證:![]() ;
;
(2)過點E作![]() 交PB于點F,連結AF,當
交PB于點F,連結AF,當![]() 時,①求證:四邊形AFEP是平行四邊形;
時,①求證:四邊形AFEP是平行四邊形;
②請判斷四邊形AFEP是否為菱形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學練習推鉛球,鉛球推出后在空中飛行的軌跡是一條拋物線,鉛球在離地面1米高的A處推出,達到最高點B時的高度是2.6米,推出的水平距離是4米,鉛球在地面上點C處著地
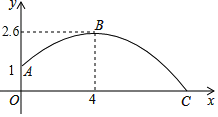
(1)根據如圖所示的直角坐標系求拋物線的解析式;
(2)這個同學推出的鉛球有多遠?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,△OBA和△DOC的邊OA、OC都在x軸的正半軸上,點B的坐標為(6,8),∠BAO![]() ∠OCD
∠OCD![]() 90°,OD
90°,OD![]() 5,CD
5,CD![]() 3.反比例函數
3.反比例函數![]() 的圖象經過點D,交AB邊于點E.
的圖象經過點D,交AB邊于點E.

(1)求k的值;(2)求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
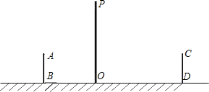
【題目】如圖,是小亮晚上在廣場散步的示意圖,圖中線段![]() 表示站立在廣場上的小亮,線段
表示站立在廣場上的小亮,線段![]() 表示直立在廣場上的燈桿,點
表示直立在廣場上的燈桿,點![]() 表示照明燈的位置.
表示照明燈的位置.
![]() 在小亮由
在小亮由![]() 處沿
處沿![]() 所在的方向行走到達
所在的方向行走到達![]() 處的過程中,他在地面上的影子長度越來越________(用“長”或“短”填空);請你在圖中畫出小亮站在
處的過程中,他在地面上的影子長度越來越________(用“長”或“短”填空);請你在圖中畫出小亮站在![]() 處的影子
處的影子![]() ;
;
![]() 當小亮離開燈桿的距離
當小亮離開燈桿的距離![]() 時,身高為
時,身高為![]() 的小亮的影長為
的小亮的影長為![]() ,
,
①燈桿的高度為多少![]() ?
?
②當小亮離開燈桿的距離![]() 時,小亮的影長變?yōu)槎嗌?/span>
時,小亮的影長變?yōu)槎嗌?/span>![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c經過A(﹣1,0)、B(5,0)、C(0,﹣5)三點.
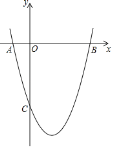
(1)求拋物線的解析式和頂點坐標;
(2)當0<x<5時,y的取值范圍為 ;
(3)點P為拋物線上一點,若S△PAB=21,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為2,點E,F分別是DC和BC兩邊上的動點且始終保持∠EAF=45°,連接AE與AF交DB于點N,M.下列結論:①△ADM∽△NBA;②△CEF的周長始終保持不變其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正確的結論是( )
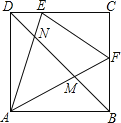
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com