
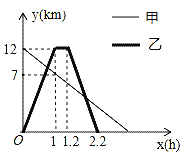
【題目】某地植物園從正門到側門有一條小路,甲徒步從正門出發勻速走向側門,乙與甲同時出發,騎自行車從側門勻速前往正門到達正門后休息0.2小時,然后按原路原速勻速返回側門,圖中折線分別表示甲、乙到側門的距離y(km)與出發時間x(h)之間的函數關系圖象,根據圖象信息解答下列問題:
(1)求甲到側門的距離y與x之間的函數關系式;
(2)求甲、乙第一次相遇時到側門的距離.
(3)求甲、乙第二次相遇的時間.
【答案】(1)y=﹣5x+12(2)![]() (3)
(3)![]()
【解析】
(1)根據函數圖象可知點(0,12)和點(1,7)在甲在休息前到側門的路程y(km)與出發時間x(h)之間的函數圖象上,從而可以解答本題;
(2)根據函數圖象可以分別求得甲乙剛開始兩端對應的函數解析式,聯立方程組即可求得甲、乙第一次相遇時到側門的距離;
(3)根據函數圖象可以得到在最后一段甲對應的函數解析式,聯立方程組即可求得甲、乙第二次相遇的時間.
(1)設甲到側門的距離y與x之間的函數關系式為y=kx+b(k≠0),
將(0,12),(1,7)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴甲到側門的距離y與x之間的函數關系式為y=﹣5x+12.
(2)設當0≤x≤1時,乙到側門的距離y與x之間的函數關系式為y=ax(a≠0),
將(1,12)代入y=ax,得:12=a,
∴當0≤x≤1時,乙到側門的距離y與x之間的函數關系式為y=12x.
聯立兩函數關系式成方程組,得:![]() ,
,
解得: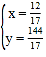 ,
,
∴甲、乙第一次相遇時到側門的距離為![]() km.
km.
(3)設當1.2≤x≤2.2時,乙到側門的距離y與x之間的函數關系式為y=mx+n(m≠0),
將(1.2,12),(2.2,0)代入y=mx+n,得:
![]() ,解得:
,解得:![]() ,
,
∴當1.2≤x≤2.2時,乙到側門的距離y與x之間的函數關系式為y=﹣12x+26.4.
聯立兩函數關系式成方程組,得:![]() ,
,
解得: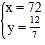 ,
,
∴甲、乙第二次相遇的時間為![]() h.
h.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出以下結論:
①b2>4ac;
②abc>0;
③2a﹣b=0;
④8a+c<0;
⑤9a+3b+c<0.
其中結論正確的是 . (填正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在2013年“崇左市初中畢業升學體育考試”測試中,參加男子擲實心球的10名考生的成績記錄如下(單位:米):7.5、6.5、8.2、7.8、8.8、8.2、8.6、8.2、8.5、9.5,則該組數據的眾數、中位數、平均數依次分別是( )
A.8.2、8.0、7.5
B.8.2、8.5、8.1
C.8.2、8.2、8.15
D.8.2、8.2、8.18
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=k1x+b交x軸于點A(﹣3,0),交y軸于點B(0,2),并與y= ![]() 的圖象在第一象限交于點C,CD⊥x軸,垂足為D,OB是△ACD的中位線.
的圖象在第一象限交于點C,CD⊥x軸,垂足為D,OB是△ACD的中位線.
(1)求一次函數與反比例函數的解析式;
(2)若點C′是點C關于y軸的對稱點,請求出△ABC′的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
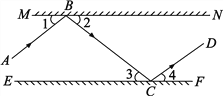
【題目】如圖所示,MN、EF分別表示兩個互相平行的鏡面,一束光線AB照射到鏡面MN上,反射光線為BC,此時∠1=∠2;光線BC經過鏡面EF反射后的光線為CD,此時∠3=∠4.試判斷AB與CD的位置關系,你是如何思考的?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC的頂點A在x軸的正半軸上,頂點C在y軸的正半軸上,OA=12,OC=9,連接AC.
(1)填空:點A的坐標: ;點B的坐標: ;
(2)若CD平分∠ACO,交x軸于D,求點D的坐標;
(3)在(2)的條件下,經過點D的直線交直線BC于E,當△CDE為以CD為底的等腰三角形時,求點E的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】溫州享有“中國筆都”之稱,其產品暢銷全球,某制筆企業欲將n件產品運往A,B,C三地銷售,要求運往C地的件數是運往A地件數的2倍,各地的運費如圖所示.設安排x件產品運往A地. 
(1)當n=200時,①根據信息填表:
A地 | B地 | C地 | 合計 | |
產品件數(件) | x | 2x | 200 | |
運費(元) | 30x |
②若運往B地的件數不多于運往C地的件數,總運費不超過4000元,則有哪幾種運輸方案?
(2)若總運費為5800元,求n的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
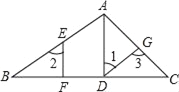
【題目】如圖,在△ABC中,AD⊥BC,垂足為D,點E在AB上,EF⊥BC,垂足為F.
(1)AD與EF平行嗎?為什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】去年暑假,某旅行社組織了一個中學生“夏令營”活動,共有253名中學生報名參加,打算選租甲、乙兩種客車載客到指定地點.甲客車2輛、乙客車1輛可坐110人,甲客車3輛、乙客車2輛可坐180人.旅行前,旅行社每輛車安排了一名帶隊老師,因此一共安排了7名帶隊老師.
(1)甲、乙兩種客車各可坐多少人?
(2)請幫助旅行社設計租車方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com