Question

【題目】（1）觀察發現：如圖1，已知Rt△ABC，∠ABC=90°，分別以AB，BC為邊，向外作正方形ABDE和正方形BCFG，連接DG．若M是DG的中點，不難發現：BM=AC．

請完善下面證明思路：①先根據 　，證明BM=DG；②再證明　 　，得到DG=AC；所以BM=AC；

（2）數學思考：若將上題的條件改為：“已知Rt△ABC，∠ABC=90°，分別以AB，AC為邊向外作正方形ABDE和正方形ACHI，N是EI的中點”，則相應的結論“AN=BC”成立嗎？

小穎通過添加如圖2所示的輔助線驗證了結論的正確性．請寫出小穎所添加的輔助線的作法，并由此證明該結論；

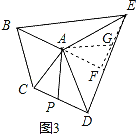
（3）拓展延伸：如圖3，已知等腰△ABC和等腰△ADE，AB=AC，AD=AE．連接BE，CD，若P是CD的中點，探索：當∠BAC與∠DAE滿足什么條件時，AP=BE，并簡要說明證明思路．

Answer 1

【答案】（1）直角三角形斜邊上的中線等于斜邊的一半，△BDG≌△BAC；（2）能，理由見解析；（3）當∠BAC=∠DAE=90°時，AP=BE，

【解析】試題分析：（1）根據題意即可得到結論；
（2）過I作IK⊥EA交EA的延長線于K，根據平角的定義得到∠BAC=∠IAK，根據全等三角形的性質得到BC=IK，AB=AK，等量代換得到AE=AI，推出AN是△EKI的中位線，于是得到結論．
（3）延長BA到F，使AF=AB，連接EF，過A作AG∥BE，根據三角形中位線的性質得到AG= BE，根據全等三角形的性質得到∠ADC=∠AEF，EF=CD，根據全等三角形的性質即可得到結論．

試題解析：

（1）①直角三角形斜邊上的中線等于斜邊的一半，②△BDG≌△BAC；

故答案為：直角三角形斜邊上的中線等于斜邊的一半，△BDG≌△BAC；

（2）能，

理由：過I作IK⊥EA交EA的延長線于K，

∵∠EAI+∠BAC=360°﹣90°﹣90°=180°，∠EAI+∠TAK=180°，

∵∠BAC=∠IAK，

在△ABC與△AKI中，，

∴△ABC≌△AKI，

∴BC=IK，AB=AK，

∵AE=AB，

∴AE=AI，

∵N是EI的中點，

∴AN是△EKI的中位線，

∴AN=IK，

∴AN=BC；

（3）當∠BAC=∠DAE=90°時，AP=BE，

延長BA到F，使AF=AB，連接EF，過A作AG∥BE，

∴EG=EF，

∴AG=BE，

∵∠BAC=∠DAE=90°，

∴∠CAD=180°﹣∠BAE，

∵∠FAE=180°﹣BAE，

∴∠CAD=∠FAE，

在△ACD與△AFE中，，

∴△ACD≌△FAE，

∴∠ADC=∠AEF，EF=CD，

∵P是CD的中點，

∴DP=CD，

∴EG=DP，

在△ADP與△AEG中，，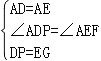

∴△ADP≌△AEG，

∴AP=AG，

∴AP=BE．