
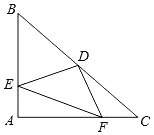
【題目】如圖,△ABC是等腰直角三角形,AB=AC,D是斜邊BC的中點,E.F分別是AB、AC邊上的點,且DE⊥DF,
(1)求證:CF=AE;
(2)若BE=8,CF=6,求線段EF的長.
【答案】(1)證明見解析;(2)10.
【解析】
(1)連接AD,根據等腰直角三角形的性質可得:∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=DC,然后利用同角的余角相等可證:∠EDA=∠CDF,然后利用ASA即可證出:△AED≌△CFD,從而證出CF=AE;
(2)根據全等三角形的性質可得:CF=AE=6,從而求出AB、AC和AF,然后根據勾股定理即可求出線段EF的長.
解:(1)連接AD,
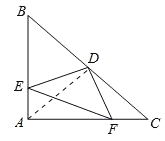
∵在Rt△ABC中,AB=AC,AD為BC邊的中線,
∴∠DAC=∠BAD=∠C=45°,AD⊥BC,AD=DC,
又∵DE⊥DF,AD⊥DC,
∴∠EDA+∠ADF=∠CDF+∠FDA=90°,
∴∠EDA=∠CDF
在△AED與△CFD中,
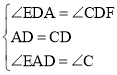 ,
,
∴△AED≌△CFD(ASA).
∴CF=AE;
(2)∵△AED≌△CFD
∴CF=AE=6,
∴AB=AE+BE=14=AC,
∴AF=AC﹣CF=8,
∴EF=![]() =
=![]() =10.
=10.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC的周長為19,點D,E在邊BC上,∠ABC的平分線垂直于AE,垂足為N,∠ACB的平分線垂直于AD,垂足為M,若BC=7,則MN的長度為( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
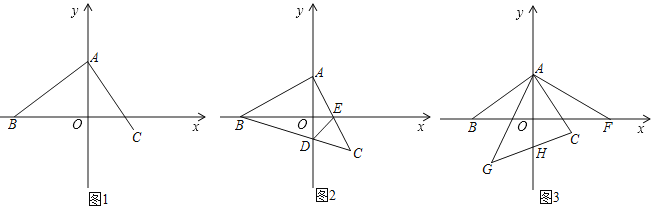
【題目】如圖,點A(0,2)在y軸上,點B在x軸上,作∠BAC=90°,并使AB=AC.
(1)如圖1,若點B的坐標為(﹣3,0),求點C的坐標.
(2)如圖2,若點B的坐標為(﹣4,0),連接BC交y軸于點D,AC交x軸于點E,連接DE,求證:BE=AD+DE.
(3)在(1)的條件下,如圖3,F為(4,0),作∠FAG=90°,并使AF=AG,連接GC交y軸于點H,求點H的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
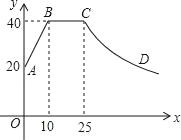
【題目】心理學家研究發現,一般情況下,一節課40分鐘中,學生的注意力隨教師講課的變化而變化.開始上課時,學生的注意力逐步增強,中間有一段時間學生的注意力保持較為理想的穩定狀態,隨后學生的注意力開始分散.經過實驗分析可知,學生的注意力指標數y隨時間x(分鐘)的變化規律如圖所示(其中AB,BC分別為線段,CD為雙曲線的一部分):
(1)分別求出線段AB和曲線CD的函數關系式;
(2)開始上課后第五分鐘時與第三十分鐘時相比較,何時學生的注意力更集中?
(3)一道數學競賽題,需要講19分鐘,為了效果較好,要求學生的注意力指標數最低達到36,那么經過適當安排,老師能否在學生注意力達到所需的狀態下講解完這道題目?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分線于M,交AB、AC于F、E,下列結論:①MB⊥BD;②FD=FB;③MD=2CE.其中一定正確的是_____.(只填寫序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016·赤峰)為有效開發海洋資源,保護海洋權益,我國對南海諸島進行了全面調查.如圖,一測量船在A島測得B島在北偏西30°方向,C島在北偏東15°方向,航行100海里到達B島,在B島測得C島在北偏東45°,求B,C兩島及A,C兩島的距離.(結果保留到整數, ![]() ≈1.41,
≈1.41, ![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共40個,小亮做摸球試驗,他將盒子內的球攪勻后從中隨機摸出一個球,記下顏色后放回,不斷重復上述過程,對試驗結果進行統計后,小玲得到下表中的數據:
摸球的次數n | 100 | 200 | 300 | 500 | 800 | 1000 | 1500 |
摸到白球的次數m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的頻率 | 0.70 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
則下列結論中正確的是( )
A. n越大,摸到白球的概率越接近0.7
B. 當n=2000時,摸到白球的次數m=1200
C. 當n很大時,摸到白球的頻率將會穩定在0.6附近
D. 這個盒子中約有28個白球
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】榮昌公司要將本公司100噸貨物運往某地銷售,經與春晨運輸公司協商,計劃租用甲,乙兩種型號的汽車共6輛,用這6輛汽車一次將貨物全部運走,其中每輛甲型汽車最多能裝該種貨物16噸,每輛乙型汽車最多能裝該種貨物18噸.已知租用1輛甲型汽車和2輛乙型汽車共需費用2500元;租用2輛甲型汽車和1輛乙型汽車共需費用2450元,且同一種型號汽車每輛租車費用相同.
(1)求租用一輛甲型汽車,一輛乙型汽車的費用分別是多少元?
(2)若榮昌公司計劃此次租車費用不超過5000元.通過計算求出該公司有幾種租車方案?請你設計出來,并求出最低的租車費用.
(3)該商業公司生產的此時令商品每件成本為15元,經過市場調研發現,這種商品在未來20天內的日銷量m(件)與時間t(天)的函數關系:m=﹣2t+100;該商品每天的價格y(元/件)與時間t(天)的函數關系為:y=![]() t+20(1≤t≤20),其中t取整數;在實際銷售的前20天中,該公司決定每銷售一件商品就捐贈a元利潤(a<4)給希望工程.公司通過銷售記錄發現,前20天中,每天扣除捐贈后的日銷售利潤時間t(天)的增大而增大(含20天的日銷售利潤和第19天的日銷售利潤相等的情況),求a的最小值.
t+20(1≤t≤20),其中t取整數;在實際銷售的前20天中,該公司決定每銷售一件商品就捐贈a元利潤(a<4)給希望工程.公司通過銷售記錄發現,前20天中,每天扣除捐贈后的日銷售利潤時間t(天)的增大而增大(含20天的日銷售利潤和第19天的日銷售利潤相等的情況),求a的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課上,老師提出如下問題:
尺規作圖:作一個角等于已知角
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB

小易同學作法如下:
①作射線O′A′;
②以點O為圓心,以任意長為半徑作弧,交OA于C,交OB于D;
③以點O′為圓心,以OC長為半徑作弧,交O′A于C
④以點C′圓心,以CD為半徑作弧,交③中所畫弧于D′;
⑤經過點D′作射線O′B′,∠A′O′B′就是所求的角.

老師說:“小易的作法正確”
請回答:小易的作圖依據是______________________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com