
【題目】已知拋物線與x軸交于A(-1,0)和B(3,0)兩點,且與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)拋物線的對稱軸方程和頂點M坐標;
(3)求四邊形ABMC的面積.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)9
;(3)9
【解析】
(1)已知了三點的坐標,可用交點式二次函數通式來設拋物線的解析式然后將C點的坐標代入拋物線中即可求出拋物線的解析式;
(2)根據(1)得出的拋物線的解析式即可求出對稱軸方程及M的坐標(可用配方法進行求解);
(3)由于四邊形ABMC不是規則的四邊形,因此可過M作x軸的垂線,將四邊形ABMC分成梯形和兩個直角三角形三部分來求.
解:(1)由題意,可設拋物線的解析式為y=a(x+1)(x3),
將C點坐標代入后可得:3=a(0+1)(03),
解得a=1,
∴拋物線的解析式為:y=(x+1)(x3)=x2+2x+3;
(2)由(1)的拋物線的解析式可知:y=x2+2x+3=(x1)2+4,
∴拋物線的對稱軸方程為:x=1,頂點M的坐標為:M(1,4);
(3)過M作MN⊥x軸于N,
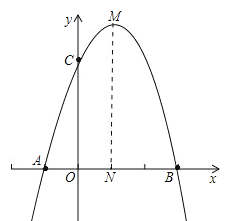
則有S四邊形ABMC=S△AOC+S△BMN+S梯形MNOC
=![]() OAOC+
OAOC+![]() BNMN+
BNMN+![]() (OC+MN)ON
(OC+MN)ON
=![]() ×1×3+
×1×3+![]() ×2×4+
×2×4+![]() ×(3+4)×1
×(3+4)×1
=9,
∴四邊形ABMC的面積為9.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,拋物線y=ax2+bx+c(a≠0)與x軸交于點A(1,0)和點B,與y軸的正半軸交于點C.現有下列結論:①abc>0;②4a﹣2b+c>0;③2a﹣b>0;④3a+c=0,其中,正確結論的個數是( )
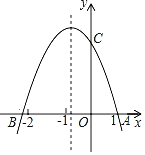
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形![]() 內接于
內接于![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() 、
、![]() 、
、![]() .
.
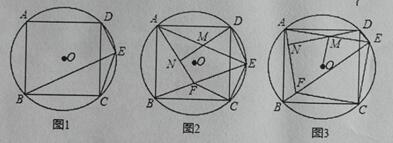
(1)如圖1,求證:∠DEC+∠BEC= 180°;
(2)如圖2,過點C作CF⊥CE交BE于點F,連接AF, M為AE的中點,連接DM并延長交AF于點N,求證: DN⊥AF;
(3)如圖3,在(2) 的條件下,連接OM,若AB=10,![]() 求OM的長.
求OM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現
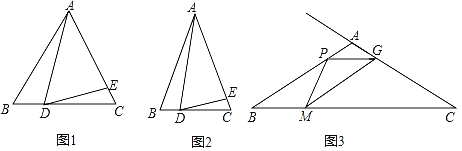
如圖1,![]() ABC是等邊三角形,點D,E分別在邊BC,AC上,若∠ADE=60°,則AB,CE,BD,DC之間的數量關系是 .
ABC是等邊三角形,點D,E分別在邊BC,AC上,若∠ADE=60°,則AB,CE,BD,DC之間的數量關系是 .
(2)拓展探究
如圖2,![]() ABC是等腰三角形,AB=AC,∠B=α,點D,E分別在邊BC,AC上.若∠ADE=α,則(1)中的結論是否仍然成立?請說明理由.
ABC是等腰三角形,AB=AC,∠B=α,點D,E分別在邊BC,AC上.若∠ADE=α,則(1)中的結論是否仍然成立?請說明理由.
(3)解決問題
如圖3,在![]() ABC中,∠B=30°,AB=AC=4cm,點P從點A出發,以1cm/s的速度沿A→B方向勾速運動,同時點M從點B出發,以
ABC中,∠B=30°,AB=AC=4cm,點P從點A出發,以1cm/s的速度沿A→B方向勾速運動,同時點M從點B出發,以![]() cm/s的速度沿B→C方向勻速運動,當其中一個點運動至終點時,另一個點隨之停止運動,連接PM,在PM右側作∠PMG=30°,該角的另一邊交射線CA于點G,連接PC.設運動時間為t(s),當△APG為等腰三角形時,直接寫出t的值.
cm/s的速度沿B→C方向勻速運動,當其中一個點運動至終點時,另一個點隨之停止運動,連接PM,在PM右側作∠PMG=30°,該角的另一邊交射線CA于點G,連接PC.設運動時間為t(s),當△APG為等腰三角形時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】伊利集團是中國規模最大、產品線最全的乳制品企業.綜合實踐小組的同學從網上搜集到如下一些伊利集團近幾年的營業狀況的資料,其中圖1是2013-2018年伊利集團營業收入及凈利潤情況統計圖,圖2是2018年伊利集團各品類業務營業、收入比例情況統計圖(數據來源:公司財報、中商產業研究院).
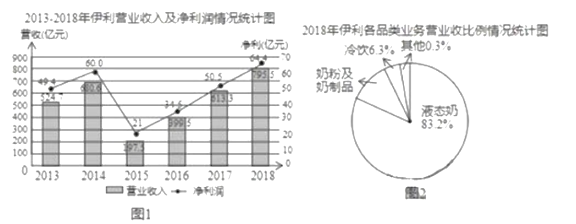
綜合實踐小組的同學結合統計圖提出了如下問題,請你解答:
(1)2018年,伊利集團營收及凈利再次刷新行業記錄,穩居亞洲乳業第一,這一年,伊利集團實現營業收入 億元,凈利潤 億元.
(2)求2018年伊利集團“奶粉及奶制品”業務的營業收入(結果精確到![]() 億元).
億元).
(3)在2013-2018這![]() 年中,伊利集團的凈利比上一年增長額最多的是 年;估計2019年伊利集團的凈利潤將比上一年增長 億元,并說明理由.
年中,伊利集團的凈利比上一年增長額最多的是 年;估計2019年伊利集團的凈利潤將比上一年增長 億元,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() 點
點![]() 是直線
是直線![]() 上的一動點(不與點
上的一動點(不與點![]() 重合),連接
重合),連接![]() 在
在![]() 的右側以
的右側以![]() 為斜邊作等腰直角三角形
為斜邊作等腰直角三角形![]() .點
.點![]() 是
是![]() 的中點,連接
的中點,連接![]() .
.
[問題發現]
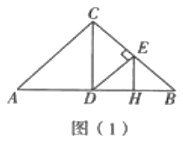
(1)如圖(1),當點![]() 是
是![]() 的中點時,線段
的中點時,線段![]() 與
與![]() 的數量關系是______,
的數量關系是______,![]() 與
與![]() 的位置關系是______;
的位置關系是______;
[猜想論證]
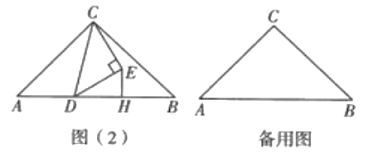
(2)如圖(2),當點![]() 在邊
在邊![]() 上且不是
上且不是![]() 的中點時,(1)中的結論是否仍然成立?若成立,請僅就圖(2)中的情況給出證明;若不成立,請說明理由.
的中點時,(1)中的結論是否仍然成立?若成立,請僅就圖(2)中的情況給出證明;若不成立,請說明理由.
[拓展應用]
(3)若![]() ,其他條件不變,連接
,其他條件不變,連接![]() .當
.當![]() 是等邊三角形時,請直接寫出
是等邊三角形時,請直接寫出![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明大學畢業回家鄉創業,第一期培植盆景與花卉各50盆售后統計,盆景的平均每盆利潤是160元,花卉的平均每盆利潤是19元,調研發現:
①盆景每增加1盆,盆景的平均每盆利潤減少2元;每減少1盆,盆景的平均每盆利潤增加2元;②花卉的平均每盆利潤始終不變.
小明計劃第二期培植盆景與花卉共100盆,設培植的盆景比第一期增加x盆,第二期盆景與花卉售完后的利潤分別為W1,W2(單位:元)
(1)用含x的代數式分別表示W1,W2;
(2)當x取何值時,第二期培植的盆景與花卉售完后獲得的總利潤W最大,最大總利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com