
【題目】如圖,在![]() 中,
中,![]() ,且點
,且點![]() 的坐標為
的坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 在
在![]() 軸的負半軸上,拋物線
軸的負半軸上,拋物線![]() 經過點
經過點![]() 和點
和點![]()

![]() 求
求![]() ,
,![]() 的值;
的值;
![]() 在拋物線的對稱軸上是否存在點
在拋物線的對稱軸上是否存在點![]() ,使得
,使得![]() 為等腰三角形?若存在,直接寫出點
為等腰三角形?若存在,直接寫出點![]() 的坐標;若不存在,請說明理由
的坐標;若不存在,請說明理由
![]() 點
點![]() 是線段
是線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸的平行線交拋物線于點
軸的平行線交拋物線于點![]() ,交
,交![]() 于點
于點![]() ,探究:當點
,探究:當點![]() 在什么位置時,四邊形
在什么位置時,四邊形![]() 是平行四邊形,此時,請判斷四邊形
是平行四邊形,此時,請判斷四邊形![]() 的形狀,并說明理由.
的形狀,并說明理由.
【答案】(1)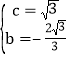 ;(2)符合題意的
;(2)符合題意的![]() 點的坐標為:
點的坐標為:![]() ;
;![]() ;
;![]() ;
;![]() ,
,![]() ;(3)四邊形
;(3)四邊形![]() 是梯形,理由見解析.
是梯形,理由見解析.
【解析】
(1)直接利用待定系數法求出拋物線解析式得出即可;
(2)利用當AQ=QC,以及當AC=Q1C時,當AC=CQ2=2![]() 時,當AQ3=AC=2
時,當AQ3=AC=2![]() 時,分別得出符合題意的答案即可;
時,分別得出符合題意的答案即可;
(3)利用平行四邊形的性質首先得出BC的長,進而表示出線段ME的長,進而求出答案,再利用梯形的判定得出答案.
![]() ∵點
∵點![]() 的坐標為
的坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 在
在![]() 軸的負半軸上,拋物線
軸的負半軸上,拋物線![]() 經過點
經過點![]() 和點
和點![]() ,
,
∴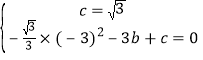 ,
,
解得: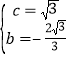 ;
;
![]() 在拋物線的對稱軸上存在點
在拋物線的對稱軸上存在點![]() ,使得
,使得![]() 為等腰三角形,
為等腰三角形,
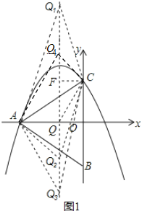
當![]() ,如圖
,如圖![]() ,
,
由![]() 得:
得:![]() ,
,
即拋物線對稱軸為:直線![]() ,則
,則![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
當![]() 時,過點
時,過點![]() 作
作![]() 直線
直線![]() ,于一點
,于一點![]() ,
,
則![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故
,故![]() 的坐標為:
的坐標為:![]() ;
;
當![]() 時,由
時,由![]() 的坐標可得;
的坐標可得;![]() ;
;
當![]() 時,則
時,則![]() ,故
,故![]() ,根據對稱性可知
,根據對稱性可知![]() (
(![]() 和
和![]() 關于
關于![]() 軸對稱)也符合題意,
軸對稱)也符合題意,
綜上所述:符合題意的![]() 點的坐標為:
點的坐標為:![]() ;
;![]() ;
;![]() ;
;![]() ,
,![]() ;
;
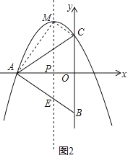
![]() 如圖
如圖![]() 所示,當四邊形
所示,當四邊形![]() 是平行四邊形,則
是平行四邊形,則![]() ,
,
∵![]() ,且點
,且點![]() 的坐標為
的坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,
,
∴![]() ,
,
則![]() ,
,
設直線![]() 的解析式為:
的解析式為:![]() ,
,
故![]() ,
,
解得: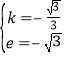 ,
,
故直線![]() 的解析式為:
的解析式為:![]() ,
,
設![]() ,
,![]() ,
,
故![]() ,
,
解得:![]() (不合題意舍去),
(不合題意舍去),![]() ,
,
故![]() 點在
點在![]() ,此時四邊形
,此時四邊形![]() 是平行四邊形;
是平行四邊形;
四邊形![]() 是梯形,
是梯形,
理由:∵四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∵![]() ,
,![]() ,
,
∴四邊形![]() 是梯形.
是梯形.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸為直線![]() .下列結論中,正確的是( )
.下列結論中,正確的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)先化簡,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】試題分析:(1)利用完全平方公式展開,化簡,代入求值. (2) 利用完全平方公式展開,化簡,整體代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
當a=-1,b=![]() 時,原式=2+2=4.
時,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【題型】解答題
【結束】
22
【題目】已知化簡(x2+px+8)(x2-3x+q)的結果中不含x2項和x3項.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,請將其分解因式;如果不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E, F在直線AC上,DF=BE, ∠AFD=∠CEB,下列條件中不能判斷△ADF≌△CBE的是( )

A.∠D=∠BB.AD=CBC.AE=CFD.AD// BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠MON=20° ,點A B分別是射線OM、ON上的動點(A、B不與點0重合),若AB![]() OM,在射線ON上有一點C,設∠OAC=x°,下列x的值不能使△ABC為等腰三角形的是( )
OM,在射線ON上有一點C,設∠OAC=x°,下列x的值不能使△ABC為等腰三角形的是( )
A.20
B.45
C.50
D.125
查看答案和解析>>
科目:初中數學 來源: 題型:
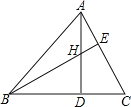
【題目】如圖,在△ABC中,高AD和BE交于點H,∠ABC=45°,BE平分∠ABC,下列結論:①∠DAC= 22.5°;②BH= 2CE; ③若連結CH,則CH⊥AB;④若CD=1,則AH=2;其中正確的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展電信事業,方便用戶,電信公司對移動電話采取不同的收費方式,其中,所使用的“便民卡”與“如意卡”在某市范圍內每月(30天)的通話時間x(min)與通話費y(元)的關系如圖所示:
(1)分別求出通話費y1,y2與通話時間x之間的函數關系式;
(2)請幫用戶計算,在一個月內使用哪一種卡便宜.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(﹣1,0),C(2,3)兩點,與y軸交于點N.其頂點為D.

(1)拋物線及直線AC的函數關系式;
(2)設點M(3,m),求使MN+MD的值最小時m的值;
(3)若拋物線的對稱軸與直線AC相交于點B,E為直線AC上的任意一點,過點E作EF∥BD交拋物線于點F,以B,D,E,F為頂點的四邊形能否為平行四邊形?若能,求點E的坐標;若不能,請說明理由;
(4)若P是拋物線上位于直線AC上方的一個動點,求△APC的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com