
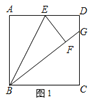
【題目】![]() 如圖
如圖![]() ,正方形
,正方形![]() 的邊長為
的邊長為![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊的中點(diǎn),將
邊的中點(diǎn),將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延長
,延長![]() 交
交![]() 邊于點(diǎn)
邊于點(diǎn)![]() ,則
,則![]() ,求出此時(shí)
,求出此時(shí)![]() 的值;
的值;
![]() 如圖
如圖![]() ,矩形
,矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊的中點(diǎn),同樣將
邊的中點(diǎn),同樣將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延長
,延長![]() 交
交![]() 邊于點(diǎn)
邊于點(diǎn)![]() .
.
①證明:![]() ;
;
②若點(diǎn)![]() 恰是
恰是![]() 邊的中點(diǎn),求
邊的中點(diǎn),求![]() 的值;
的值;
③若![]() 與
與![]() 相似,求
相似,求![]() 的值.
的值.

【答案】![]()
![]() ;
;![]() ①見解析;②
①見解析;②![]() ,③
,③![]() .
.
【解析】
(1)首先設(shè)DG為x,則由正方形的性質(zhì)即可求得BG與CG的值,利用勾股定理構(gòu)造方程,解方程即可求得DG的值;
(2)①首先連接EG,由△FBE是由△ABE翻折得到的,利用HL,即可求得Rt△EFG≌Rt△EDG,則可證得DG=FG;
②由G是CD的中點(diǎn),得到DG與CG的值,在Rt△BCG中,利用勾股定理即可求得AD的長;
③由平行線與翻折變換的性質(zhì),易得:∠ABE=![]() ∠CGB,又由相似三角形的性質(zhì)與三角函數(shù)的性質(zhì),即可求得AD的值.
∠CGB,又由相似三角形的性質(zhì)與三角函數(shù)的性質(zhì),即可求得AD的值.
![]() 解:設(shè)
解:設(shè)![]() 為
為![]() ,
,
由題意得:![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
有:![]() ,
,
解得:![]() .
.
∴![]() ;
;![]() ①證明:連接
①證明:連接![]() ,
,
∵![]() 是由
是由![]() 翻折得到的,
翻折得到的,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ;
;
②解:若![]() 是
是![]() 的中點(diǎn),則
的中點(diǎn),則![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
③解:由題意![]() ,
,
∴![]() .
.
∵![]() 是由
是由![]() 翻折得到的,
翻折得到的,
∴![]() ,
,
∴![]() .
.
∴若![]() 與
與![]() 相似,則必有
相似,則必有![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為發(fā)展電信事業(yè),方便用戶,電信公司對移動電話采取不同的收費(fèi)方式,其中,所使用的“便民卡”與“如意卡”在某市范圍內(nèi)每月(30天)的通話時(shí)間x(min)與通話費(fèi)y(元)的關(guān)系如圖所示:
(1)分別求出通話費(fèi)y1,y2與通話時(shí)間x之間的函數(shù)關(guān)系式;
(2)請幫用戶計(jì)算,在一個(gè)月內(nèi)使用哪一種卡便宜.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+c與一直線相交于A(﹣1,0),C(2,3)兩點(diǎn),與y軸交于點(diǎn)N.其頂點(diǎn)為D.

(1)拋物線及直線AC的函數(shù)關(guān)系式;
(2)設(shè)點(diǎn)M(3,m),求使MN+MD的值最小時(shí)m的值;
(3)若拋物線的對稱軸與直線AC相交于點(diǎn)B,E為直線AC上的任意一點(diǎn),過點(diǎn)E作EF∥BD交拋物線于點(diǎn)F,以B,D,E,F為頂點(diǎn)的四邊形能否為平行四邊形?若能,求點(diǎn)E的坐標(biāo);若不能,請說明理由;
(4)若P是拋物線上位于直線AC上方的一個(gè)動點(diǎn),求△APC的面積的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
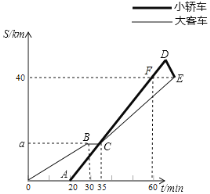
【題目】初二![]() 班同學(xué)從學(xué)校出發(fā)去某自然保護(hù)區(qū)研學(xué)旅行,一部分乘坐大客車先出發(fā),余下的幾人20分鐘后乘坐小轎車沿同一路線出行
班同學(xué)從學(xué)校出發(fā)去某自然保護(hù)區(qū)研學(xué)旅行,一部分乘坐大客車先出發(fā),余下的幾人20分鐘后乘坐小轎車沿同一路線出行![]() 大客車中途停車等候,小轎車趕上來之后,大客車以出發(fā)時(shí)速度的
大客車中途停車等候,小轎車趕上來之后,大客車以出發(fā)時(shí)速度的![]() 繼續(xù)行駛,小轎車保持原速度不變
繼續(xù)行駛,小轎車保持原速度不變![]() 小轎車司機(jī)因路線不熟錯(cuò)過了景點(diǎn)入口,再原路提速返回,恰好與大客車同時(shí)到達(dá)景點(diǎn)入口
小轎車司機(jī)因路線不熟錯(cuò)過了景點(diǎn)入口,再原路提速返回,恰好與大客車同時(shí)到達(dá)景點(diǎn)入口![]() 兩車距學(xué)校的路程
兩車距學(xué)校的路程![]() 單位:千米
單位:千米![]() 和行駛時(shí)間
和行駛時(shí)間![]() 單位:分鐘
單位:分鐘![]() 之間的函數(shù)關(guān)系如圖所示.
之間的函數(shù)關(guān)系如圖所示.
請結(jié)合圖象解決下面問題:
![]() 學(xué)校到景點(diǎn)的路程為______千米,大客車途中停留了______分鐘,
學(xué)校到景點(diǎn)的路程為______千米,大客車途中停留了______分鐘,![]() ______千米;
______千米;
![]() 在小轎車司機(jī)駛過景點(diǎn)入口時(shí),大客車離景點(diǎn)入口還有多遠(yuǎn)?
在小轎車司機(jī)駛過景點(diǎn)入口時(shí),大客車離景點(diǎn)入口還有多遠(yuǎn)?
![]() 若大客車一直以出發(fā)時(shí)的速度行駛,中途不再停車,那么小轎車折返后到達(dá)景點(diǎn)入口,需等待______分鐘,大客車才能到達(dá)景點(diǎn)入口.
若大客車一直以出發(fā)時(shí)的速度行駛,中途不再停車,那么小轎車折返后到達(dá)景點(diǎn)入口,需等待______分鐘,大客車才能到達(dá)景點(diǎn)入口.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四邊形ABCD中,∠A=140°,∠D=80°.

(1)如圖1,若∠B=∠C,試求出∠C的度數(shù);
(2)如圖2,若∠ABC的角平分線BE交DC于點(diǎn)E,且BE∥AD,試求出∠C的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
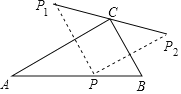
【題目】如圖,△ABC中,∠ACB=90°,∠A=30°,AC=6,點(diǎn)P在邊AB上運(yùn)動(不與端點(diǎn)重合),點(diǎn)P關(guān)于直線AC,BC對稱的點(diǎn)分別為P1,P2.則在點(diǎn)P的運(yùn)動過程中,線段P1P2的長度m的取值范圍是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,若△ABC內(nèi)一點(diǎn)P,滿足∠PAB=∠PBC=∠PCA=α,則稱點(diǎn)P為△ABC的布洛卡點(diǎn).通過研究一些特殊三角形中的布洛卡點(diǎn),得到如下兩個(gè)結(jié)論:
①若∠BAC=90°,則必有∠APC=90°;②若AB=AC,則必有∠APB=∠BPC.
對于這兩個(gè)結(jié)論,下列說法正確的是( )
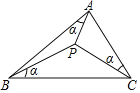
A.①對,②錯(cuò)B.①錯(cuò),②對C.①,②均錯(cuò)D.①,②均對
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,等腰三角形ABC的底邊BC長為4,面積是12,腰AB的垂直平分線EF分別交AB,AC于點(diǎn)E、F,若點(diǎn)D為底邊BC的中點(diǎn),點(diǎn)M為線段EF上一動點(diǎn),則△BDM的周長的最小值為_____.
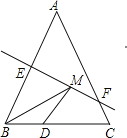
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,AB∥DE,AC∥DF,AC=DF下列條件中,不能判斷△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com