
【題目】在一個三角形中,各邊和它所對角的正弦的比相等.即![]() .利用上述結論可以求解如下題目.如:
.利用上述結論可以求解如下題目.如:
在![]() 中,若∠A=45°,∠B=30°,a=6,求b.
中,若∠A=45°,∠B=30°,a=6,求b.
【答案】(1)![]() 是等邊三角形,證明見解析;
是等邊三角形,證明見解析;
(2)![]()
試題分析:(1)先根據路程=速度×時間求出A1A2=30![]() ×
×![]() =10
=10![]() ,又A2B2=10
,又A2B2=10![]() ,∠A1A2B2=60°,根據有一個角是60°的等腰三角形是等邊三角形即可得出△A1A2B2是等邊三角形;(2)先由平行線的性質及方向角的定義求出∠A1B1B2=75°-15°=60°,由等邊三角形的性質得出∠A2A1B2=60°,A1B2=A1A2=10
,∠A1A2B2=60°,根據有一個角是60°的等腰三角形是等邊三角形即可得出△A1A2B2是等邊三角形;(2)先由平行線的性質及方向角的定義求出∠A1B1B2=75°-15°=60°,由等邊三角形的性質得出∠A2A1B2=60°,A1B2=A1A2=10![]() ,那么∠B1A1B2=105°-60°=45°.然后在△B1A1B2中,根據閱讀材料可知,
,那么∠B1A1B2=105°-60°=45°.然后在△B1A1B2中,根據閱讀材料可知, ![]() ,求出B1B2的距離,再由時間求出乙船航行的速度.
,求出B1B2的距離,再由時間求出乙船航行的速度.
試題解析:(1) ![]() 是等邊三角形,理由如下:
是等邊三角形,理由如下:
連結A1B2.
∵甲船以每小時30![]() 海里的速度向正北方向航行,航行20分鐘到達A2,
海里的速度向正北方向航行,航行20分鐘到達A2,
∴A1A2=30![]() ×
×![]() =10
=10![]() ,
,
又∵A2B2=10![]() ,∠A1A2B2=60°,
,∠A1A2B2=60°,
∴△A1A2B2是等邊三角形;
(2)過點B作B1N∥A1A2,如圖,

∵B1N∥A1A2,
∴∠A1B1N=180°∠B1A1A2=180°105°=75°,
∴∠A1B1B2=75°15°=60°.
∵△A1A2B2是等邊三角形,
∴∠A2A1B2=60°,A1B2=A1A2=10![]()
∴∠B1A1B2=105°60°=45°.
在△B1A1B2中,
∵A1B2=10![]() ,∠B1A1B2=45°,∠A1B1B2=60°,
,∠B1A1B2=45°,∠A1B1B2=60°,
由閱讀材料可知, ![]() ,
,
解得B1B2= ,
,
所以乙船每小時航行: ![]() ÷
÷![]() =
= ![]() 海里。
海里。


科目:初中數學 來源: 題型:
【題目】某中學初三(6)班十幾名同學畢業前和數學老師合影留念,一張彩色底片要0.6元,擴印一張相片0.5元,每人分一張,免費贈送老師一張(由學生出錢),每個學生交0.6元剛好,則相片上共有______人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.點P以每秒一個單位長度的速度沿著B-C-A運動, ![]() 始終與AB相切,設點P運動的時間為t,0P的面積為y.則y與t之間的函效關系圖像大致是( )
始終與AB相切,設點P運動的時間為t,0P的面積為y.則y與t之間的函效關系圖像大致是( )

A.  B.
B. 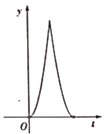 C.
C. 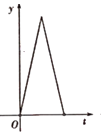 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系xOy中,平行四邊形ABCD四個頂點的坐標分別為A(1,1),B(4,1),C(5,2),D(2,2),直線l:y=kx+b與直線y=﹣2x平行.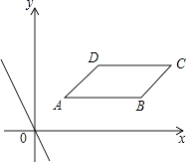

(1)若直線l過點D,求直線l的解析式;
(2)若直線l同時與邊AB和CD都相交,求b的取值范圍;
(3)若直線l沿線段AC從點A平移至點C,設直線l與x軸的交點為P,問是否存在一點P,使△PAB為等腰三角形?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
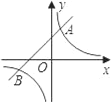
【題目】已知:如圖,反比例函數y=![]() 的圖象與一次函數y=mx+b的圖象交于A(1,3),B(n,﹣1)兩點.
的圖象與一次函數y=mx+b的圖象交于A(1,3),B(n,﹣1)兩點.
(1)求反比例函數與一次函數的解析式;
(2)根據圖象回答:當x取何值時,反比例函數的值大于一次函數的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解本校九年級學生期末數學考試情況,小亮在九年級隨機抽取了一部分學生的期末數學成績為樣本,分為A、B(89~80分)、C(79~60分)、D(59~0分)四個等級進行統計,并將統計結果繪制成如下統計圖,請你根據統計圖解答以下問題:
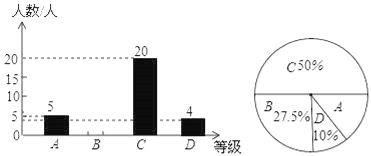
(1)這次隨機抽取的學生共有多少人?
(2)請補全條形統計圖;
(3)這個學校九年級共有學生1200人,若分數為80分(含80分)以上為優秀,請估計這次九年級學生期末數學考試成績為優秀的學生人數大約有多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com