
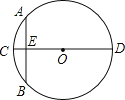
【題目】“圓材埋壁”是我國古代著名數學著作《九章算術》中的問題:“今有圓材,埋在壁中,不知大小,以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?”用數學語言可表述為:“如圖,CD為⊙O的直徑,弦AB⊥CD于E,CE=1寸,AB=10寸,求直徑CD的長”.(1尺=10寸)則CD=_____.
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
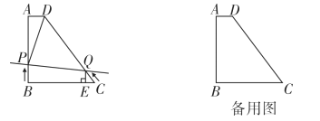
(1)求四邊形![]() 的面積
的面積![]() ;
;
(2)動點![]() 從點
從點![]() 出發,以每秒1個單位長度的速度,沿
出發,以每秒1個單位長度的速度,沿![]() 方向,向點
方向,向點![]() 運動;動點
運動;動點![]() 從點
從點![]() 出發,以每秒1個單位長度的速度,沿
出發,以每秒1個單位長度的速度,沿![]() 方向,向點
方向,向點![]() 運動,過點
運動,過點![]() 作
作![]() 于點
于點![]() .若
.若![]() 、
、![]() 兩點同時出發,當其中一點到達目的地時整個運動隨之結束,設運動時間為
兩點同時出發,當其中一點到達目的地時整個運動隨之結束,設運動時間為![]() .問:
.問:
①當點![]() 在
在![]() 上運動時,是否存在這樣的
上運動時,是否存在這樣的![]() ,使得直線
,使得直線![]() 將四邊形
將四邊形![]() 的周長平分?若存在,請求出
的周長平分?若存在,請求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
②在運動過程中,是否存在這樣的![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出所有符合條件的
相似?若存在,請求出所有符合條件的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊三角形ABC邊長是定值,點O是它的外心,過點O任意作一條直線分別交AB,BC于點D,E.將△BDE沿直線DE折疊,得到△B′DE,若B′D,B′E分別交AC于點F,G,連接OF,OG,則下列判斷錯誤的是( )
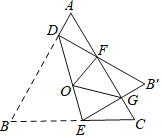
A. △ADF≌△CGE
B. △B′FG的周長是一個定值
C. 四邊形FOEC的面積是一個定值
D. 四邊形OGB'F的面積是一個定值
查看答案和解析>>
科目:初中數學 來源: 題型:
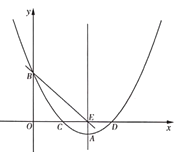
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,過拋物線的頂點
,過拋物線的頂點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,垂足為點
,垂足為點![]() ,作直線
,作直線![]() .
.
(1)求直線![]() 的解析式;
的解析式;
(2)點![]() 為第一象限內直線
為第一象限內直線![]() 上的一點,連接
上的一點,連接![]() ,取
,取![]() 的中點
的中點![]() ,作射線
,作射線![]() 交拋物線于點
交拋物線于點![]() ,設線段
,設線段![]() 的長為
的長為![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]() ,求
,求![]() 與
與![]() 之間的函數關系式(不要求寫出自變量
之間的函數關系式(不要求寫出自變量![]() 的取值范圍);
的取值范圍);
(3)在(2)的條件下,在線段![]() 上有一點
上有一點![]() ,連接
,連接![]() ,
,![]() ,線段
,線段![]() 交線段
交線段![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經中共中央決定設立河北雄安新區,這一重大措施必將帶動首都及周邊區域向更高水平發展,同時也會帶來更多商機.某水果經銷商在第一周購進一批水果1160件,預計在第二周進行試銷,購進價格為每件10元,若售價為每件12元,則可全部售出;若售價每漲價0.1元,銷量就減少2件.
(1)若該經銷商在第二周的銷量不低于1100件,則售價應不高于多少元?
(2)由于銷量較好,第三周水果進價比第一周每件增加了20%,該經銷商增加了進貨量,并加強了宣傳力度,結果第三周的銷量比第二周在(1)條件下的最低銷量增加了m%,但售價比第二周在(1)條件下的最高售價減少了![]() m%,結果第三周利潤達到3388元,求m的值(m>10).
m%,結果第三周利潤達到3388元,求m的值(m>10).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是等邊三角形,以AB為直徑作⊙O,交BC邊于點D,交AC邊于點F,作DE⊥AC于點E.
(1)求證:DE是⊙O的切線;
(2)若△ABC的邊長為4,求EF的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個轉盤.轉盤分成8個相同的圖形,顏色分為紅、綠、黃三種.指針的位置固定,轉動轉盤后任其茲有停止,其中的某個扇形會恰好停在指針所指的位置(指針指向兩個圖形的交線時,當作指向右邊的圖形).求下列事件的概率:
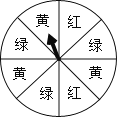
(1)指針指向紅色;
(2)指針指向黃色或綠色。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=x+m圖象過點A(1,0),交y軸于點![]() ,
,![]() 為y軸負半軸上一點,且
為y軸負半軸上一點,且![]() ,過
,過![]() 、
、![]() 兩點的拋物線交直線
兩點的拋物線交直線![]() 于點
于點![]() ,且CD//x軸.
,且CD//x軸.
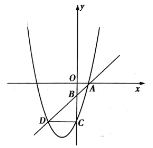
(1)求這條拋物線的解析式;
(2)觀察圖象,寫出使一次函數值小于二次函數值時![]() 的取值范圍;
的取值范圍;
(3)在題中的拋物線上是否存在一點![]() ,使得
,使得![]() 為直角?若存在,求出點
為直角?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB和拋物線的交點是A(0,﹣3),B(5,9),已知拋物線的頂點D的橫坐標是2.
(1)求拋物線的解析式及頂點坐標;
(2)在x軸上是否存在一點C,與A,B組成等腰三角形?若存在,求出點C的坐標,若不在,請說明理由;
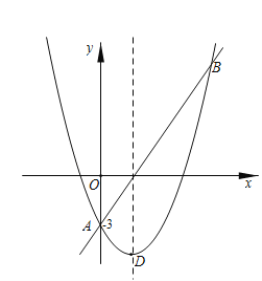
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com