
【題目】在平面直角坐標系中,分別過點A(m,0),B(m+2,0)作垂直于x軸的直線l1和l2,探究直線 l1、l2與函數(shù)y=![]() 的圖像(雙曲線)之間的關系,下列結論錯誤的是( )
的圖像(雙曲線)之間的關系,下列結論錯誤的是( )
A.兩條直線中總有一條與雙曲線相交
B.當 m=1 時,兩條直線與雙曲線的交點到原點的距離相等
C.當 m<0 時,兩條直線與雙曲線的交點都在 y 軸左側
D.當 m>0 時,兩條直線與雙曲線的交點都在 y 軸右側
【答案】C
【解析】
反比例函數(shù)y=![]() 的圖象位于第一、三象限,過點A(m,0),B(m+2,0)垂直于x軸的直線l1和l2根據(jù)m的值分別討論各種情況,并對選項做出判斷.
的圖象位于第一、三象限,過點A(m,0),B(m+2,0)垂直于x軸的直線l1和l2根據(jù)m的值分別討論各種情況,并對選項做出判斷.
解:反比例函數(shù)y=![]() 的圖象位于第一、三象限,過點A(m,0),B(m+2,0)垂直于x軸的直線l1和l2
的圖象位于第一、三象限,過點A(m,0),B(m+2,0)垂直于x軸的直線l1和l2
無論m為何值,直線l1和l2至少由一條與雙曲線相交,因此A正確;
當m=1時,直線l1和l2與雙曲線的交點為(1,3)(3,1)它們到原點的距離為![]() ,因此B是正確的;
,因此B是正確的;
當m<0時,但m+2的值不能確定,因此兩條直線與雙曲線的交點不一定都在y軸的左側,因此C選項是不正確的;
當m>0時,m+2>0,兩條直線與雙曲線的交點都在y軸右側,是正確的,
故選:C.


科目:初中數(shù)學 來源: 題型:
【題目】感知與填空:如圖①,直線![]() ,求證:
,求證:![]() .
.

閱讀下面的解答過程,并填上適當?shù)睦碛桑?/span>
解:過點![]() 作直線
作直線![]() ,
,
![]() ( )
( )
![]() (已知),
(已知),![]() ,
,
![]() ( )
( )
![]() ( )
( )
![]() ,
,
![]() ( )
( )
應用與拓展:如圖②,直線![]() ,若
,若![]() .
.

則![]() 度
度
方法與實踐:如圖③,直線![]() ,若
,若![]() ,則
,則![]() 度.
度.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,A(﹣![]() ,0)、B(0,1)分別為x軸、y軸上的點,△ABC為等邊三角形,點P(3,a)在第一象限內,且滿足2S△ABP=S△ABC,則a的值為( )
,0)、B(0,1)分別為x軸、y軸上的點,△ABC為等邊三角形,點P(3,a)在第一象限內,且滿足2S△ABP=S△ABC,則a的值為( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】初一(1)班針對“你最喜愛的課外活動項目”對全班學生進行調查(每名學生分別選一個活動項目),并根據(jù)調查結果列出統(tǒng)計表,繪制成扇形統(tǒng)計圖.

根據(jù)以上信息解決下列問題:
(1)![]() ,
,![]() ;
;
(2)扇形統(tǒng)計圖中機器人項目所對應扇形的圓心角度數(shù)為 ![]() ;
;
(3)從選航模項目的![]() 名學生中隨機選取
名學生中隨機選取![]() 名學生參加學校航模興趣小組訓練,請用列舉法(畫樹狀圖或列表)求所選取的
名學生參加學校航模興趣小組訓練,請用列舉法(畫樹狀圖或列表)求所選取的![]() 名學生中恰好有
名學生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】A、B兩地相距90km,甲、乙兩人從兩地出發(fā)相向而行,甲先出發(fā).圖中l1,l2表示兩人離A地的距離S(km)與時間t(h)的關系,結合圖像回答下列問題.

(1)表示甲離A地的距離與時間關系的圖像是___(填l1或l2)乙的速度是___km/h;
(2)求出l2的函數(shù)關系式,并注明自變量t的取值范圍;
(3)甲出發(fā)后多少時間兩人恰好相距15km?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某旅游景點有三種門票:成人票、兒童票和團購票,團購票價低于成人票、高于兒童票,但一次性購票需達到一定的數(shù)量![]() 某旅游團有8名兒童,若購買該景點的成人票和兒童票共需3040元,其中成人票總費用是兒童票總費用的
某旅游團有8名兒童,若購買該景點的成人票和兒童票共需3040元,其中成人票總費用是兒童票總費用的![]() 倍;若視兒童為成人,并再多買2張門票,即可達到景點團購的數(shù)量要求,旅游團按團購票購票總費用可節(jié)約40元.
倍;若視兒童為成人,并再多買2張門票,即可達到景點團購的數(shù)量要求,旅游團按團購票購票總費用可節(jié)約40元.
![]() 求該景點兒童門票的單價;
求該景點兒童門票的單價;
![]() 若5張成人票費用與6張團購票費用相同,求這個旅游團的總人數(shù)和該景點成人門票的單價?
若5張成人票費用與6張團購票費用相同,求這個旅游團的總人數(shù)和該景點成人門票的單價?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】兩組數(shù)據(jù):98,99,99,100和98.5,99,99,99.5,則關于以下統(tǒng)計量說法不正確的是( )
A. 平均數(shù)相等
B. 中位數(shù)相等
C. 眾數(shù)相等
D. 方差相等
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(1)如圖1,將一矩形紙片ABCD沿著EF折疊,CE交AF于點G,過點G作GH∥EF,交線段BE于點H.

①判斷EG與EH是否相等,并說明理由.
②判斷GH是否平分∠AGE,并說明理由.
(2)如圖2,如果將(1)中的已知條件改為折疊三角形紙片ABC,其它條件不變.
①判斷EG與EH是否相等,并說明理由.
②判斷GH是否平分∠AGE,如果平分,請說明理由;如果不平分,請用等式表示∠EGH,∠AGH與∠C的數(shù)量關系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
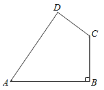
(1)判斷∠D是否是直角,并說明理由.
(2)求四邊形ABCD的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com