
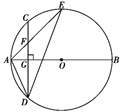
【題目】如圖,AB是☉O的直徑,弦CD⊥AB于點G,點F是CD上一點,且滿足![]() =
=![]() ,連接AF并延長交☉O于點E,連接AD、DE,若CF=2,AF=3.給出下列結論:①△ADF∽△AED;②FG=3;③tan∠E=
,連接AF并延長交☉O于點E,連接AD、DE,若CF=2,AF=3.給出下列結論:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正確結論的個數是( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】分析:①利用垂徑定理可知![]() ,可知∠ADF=∠AED,結合公共角可證明△ADF∽△AED;②結合CF=2,且
,可知∠ADF=∠AED,結合公共角可證明△ADF∽△AED;②結合CF=2,且![]() ,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=
,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=![]() ,且∠E=∠ADG,可判斷出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7
,且∠E=∠ADG,可判斷出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7![]() .
.
詳解:①∵AB為直徑,AB⊥CD,
∴![]() ,
,
∴∠ADF=∠AED,且∠FAD=∠DAE,
∴△ADF∽△AED,
∴①正確;
②∵AB為直徑,AB⊥CD,
∴CG=DG,
∵![]() ,且CF=2,
,且CF=2,
∴FD=6,
∴CD=8,
∴CG=4,
∴FG=CG-CF=4-2=2,
∴②錯誤;
③在Rt△AGF中,AF=3,FG=2,
∴AG=![]() ,且DG=4,
,且DG=4,
∴tan∠ADG=![]() ,
,
∵∠E=∠ADG,
∴tan∠E=![]() ,
,
∴③錯誤;
④在Rt△ADG中,AG=![]() ,DG=4,
,DG=4,
∴AD=![]() ,
,
∴![]() ,
,
∴△ADF∽△AED中的相似比為![]() ,
,
∴![]() ,
,
在△ADF中,DF=6,AG=![]() ,
,
∴S△ADF=![]() DFAG=
DFAG=![]() ×6×
×6×![]() =3
=3![]() ,
,
∴![]() ,
,
∴S△ADE=7![]() ,
,
∴④錯誤;
∴正確的有①一個.
故選:A.


科目:初中數學 來源: 題型:
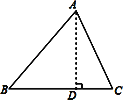
【題目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面積.
某學習小組經過合作交流,給出了下面的解題思路:

(1)請你按照他們的解題思路過程完成解答過程;
(2)填空:在△DEF中,DE=15,EF=13,DF=4,則△DEF的面積是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了了解本校學生喜愛的球類運動,在本校范圍內隨機調查了部分學生,將收集的 數據繪制成如下兩幅不完整的統計圖.請你根據圖中提供的信息解答下列問題:

(1)本次一共調查了多少名學生?
(2)補全條形統計圖,并求出“足球”在扇形統計圖中所占圓心角的度數;
(3)若已知該校有 500 名學生,請你根據調查的結果估計愛好“足球”和“排球”的學生共有多 少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正比例函數y=2x和反比例函數的圖象交于點A(m,﹣2).

(1)求反比例函數的解析式;
(2)觀察圖象,直接寫出正比例函數值大于反比例函數值時自變量x的取值范圍;
(3)若雙曲線上點C(2,n)沿OA方向平移![]() 個單位長度得到點B,判斷四邊形OABC的形狀并證明你的結論.
個單位長度得到點B,判斷四邊形OABC的形狀并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.了解全國中學生最喜愛哪位歌手,適合全面調查.
B.甲乙兩種麥種,連續3年的平均畝產量相同,它們的方差為:S甲2=5,S乙2=0.5,則甲麥種產量比較穩.
C.某次朗讀比賽中預設半數晉級,某同學想知道自己是否晉級,除知道自己的成績外,還需要知道平均成績.
D.一組數據:3,2,5,5,4,6的眾數是5.
查看答案和解析>>
科目:初中數學 來源: 題型:
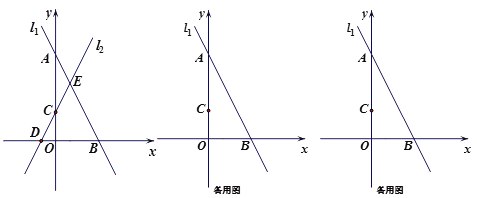
【題目】在平面直角坐標系中,直線l1:![]() 與坐標軸交于A,B兩點,直線l2:
與坐標軸交于A,B兩點,直線l2:![]() (
(![]() ≠0)與坐標軸交于點C,D.
≠0)與坐標軸交于點C,D.
(1)求點A,B的坐標;
(2)如圖,當![]() =2時,直線l1,l2與相交于點E,求兩條直線與
=2時,直線l1,l2與相交于點E,求兩條直線與![]() 軸圍成的△BDE的面積;
軸圍成的△BDE的面積;
(3)若直線l1,l2與![]() 軸不能圍成三角形,點P(a,b)在直線l2:
軸不能圍成三角形,點P(a,b)在直線l2:![]() (k≠0)上,且點P在第一象限.
(k≠0)上,且點P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
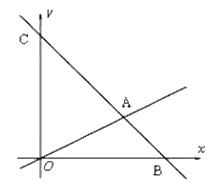
【題目】如圖,在平面直角坐標系中,過點B(6,0)的直線AB與![]() 軸相交于點C(0,6),與直線OA相交于點A且點A縱坐標為2,動點P沿路線O
軸相交于點C(0,6),與直線OA相交于點A且點A縱坐標為2,動點P沿路線O![]() A
A![]() C運動.
C運動.
(1)求直線BC的解析式.
(2)求![]() 的面積.
的面積.
(3)當![]() 的面積是
的面積是![]() 的面積的
的面積的![]() 時,求出這時點P的坐標.
時,求出這時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com