
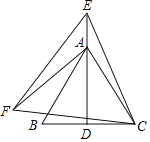
【題目】如圖,D為等邊△ABC中邊BC的中點,在邊DA的延長線上取一點E,以CE為邊、在CE的左下方作等邊△CEF,連結AF.若AB=4,AF=![]() ,則CF的值為_____.
,則CF的值為_____.
【答案】![]() .
.
【解析】
連接BF,由等邊三角形的性質得出AB=AC=BC=4,CE=CF,∠ABC=∠ACB=∠BAC=∠ECF=60°,得出∠BCF=∠ACE,證明△BCF≌△ACE(SAS),得出∠CBF=∠CAE,由等邊三角形的性質得出AD⊥BC,∠CAD=![]() ∠BAC=30°,由直角三角形的性質得出CD=
∠BAC=30°,由直角三角形的性質得出CD=![]() AC=2,AD=
AC=2,AD=![]() CD=2
CD=2![]() ,求出∠CAE=∠CBF=150°,得出∠ABF=90°,由勾股定理得出BF=
,求出∠CAE=∠CBF=150°,得出∠ABF=90°,由勾股定理得出BF=![]() ,得出DE=AD+AE=
,得出DE=AD+AE=![]() ,再由勾股定理即可得出答案.
,再由勾股定理即可得出答案.
解:連接BF,如圖所示:
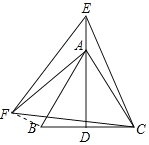
∵△ABC和△CEF是等邊三角形,
∴AB=AC=BC=4,CE=CF,∠ABC=∠ACB=∠BAC=∠ECF=60°,
∴∠BCF=∠ACE,
在△BCF和△ACE中,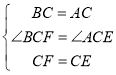 ,
,
∴△BCF≌△ACE(SAS),
∴∠CBF=∠CAE,
∵D為等邊△ABC中邊BC的中點,
∴AD⊥BC,∠CAD=![]() ∠BAC=30°,
∠BAC=30°,
∴CD=![]() AC=2,AD=
AC=2,AD=![]() CD=2
CD=2![]() ,∠CAE=150°,
,∠CAE=150°,
∴∠CBF=150°,
∴∠ABF=150°﹣60°=90°,
∴BF=![]() =
=![]() =
=![]() ,
,
∴AE=![]() ,
,
∴DE=AD+AE=3![]() ,
,
∴CF=CE=![]() =
=![]() =
=![]() ;
;
故答案為:![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】某地發(fā)生8.1級強烈地震,我國積極組織搶險隊赴地震災區(qū)參與搶險工作.如圖,某探測隊在地面A,B兩處均探測出建筑物下方C處有生命跡象,已知探測線與地面的夾角分別是25°和60°,且AB=4米,求該生命跡象所在位置C的深度.(結果精確到1米.參考數(shù)據(jù):sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABCO的頂點O為坐標原點,邊CO在x軸正半軸上,∠AOC=60°,反比例函數(shù)y=![]() (x>0)的圖象經過點A,交菱形對角線BO于點D,DE⊥x軸于點E,則CE長為( )
(x>0)的圖象經過點A,交菱形對角線BO于點D,DE⊥x軸于點E,則CE長為( )

A. 1 B. ![]() C. 2
C. 2![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】材料:一般地,若![]() (
(![]() 且
且![]() ),那么
),那么![]() 叫做以
叫做以![]() 為底
為底![]() 的對數(shù),記作
的對數(shù),記作![]() ,比如指數(shù)式
,比如指數(shù)式![]() 可以轉化為對數(shù)式
可以轉化為對數(shù)式![]() ,對數(shù)式
,對數(shù)式![]() 可以轉化為指數(shù)式
可以轉化為指數(shù)式![]() .
.
根據(jù)以上材料,解決下列問題:
(1)計算:![]() ,
,![]() ,
,![]() ;
;
(2)觀察(1)中的三個數(shù),猜測:![]() (
(![]() 且
且![]() ,
,![]() ,
,![]() ),并加以證明這個結論;
),并加以證明這個結論;
(3)已知:![]() ,求
,求![]() 和
和![]() 的值(
的值(![]() 且
且![]() ).
).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,BC=5,點E是邊CD的中點,將△ADE沿AE折疊后得到△AFE.延長AF交邊BC于點G,則CG為_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的方格紙中,把△ABC向右平移5個方格得△A1B1C1,再繞點B1順時針方向旋轉90°得△A2B1C2.
(1)畫出平移和旋轉后的圖形,并標明對應字母.

(2)求頂點A從開始到結束所經過的路徑的長.(結果用含有π的式子表示)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某城區(qū)近幾年通過拆遷舊房,植草,栽樹,修建公園等措施,使城區(qū)綠地面積不斷增加。
(1)根據(jù)圖中所提供的信息,回答下列問題:2008年綠地面積為 公頃。
在2006、2007、2008年這三年中,綠地面積增加最多的是 年。
(2)為了滿足城市發(fā)展的需要,計劃到2010年使綠地總面積達到72.6公頃,試求這兩年(2008——2010)綠地面積的年平均增長率。

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知△ABC在平面直角坐標系中的位置如圖所示.
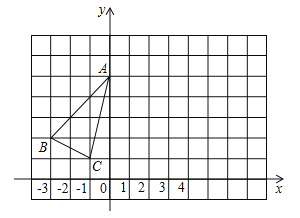
(1)畫出△ABC關于y軸對稱的△AB1C1, 并寫出B1的坐標;
(2)將△ABC向右平移8個單位, 畫出平移后的△A2B2C2, 寫出B2的坐標;
(3)認真觀察所作的圖形, △AB1C1與△A2B2C2有怎樣的位置關系.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠BAC=90°,D是AC的中點,CE⊥BD于點E,交BA的延長線于點F.若BF=12,則△FBC的面積為( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com