
【題目】如圖,一次函數yx3的圖象與反比例函數y![]() (k為常數,且k0)的圖象交于A(1,a),B兩點.
(k為常數,且k0)的圖象交于A(1,a),B兩點.
(1)求反比例函數的表達式及點B的坐標;
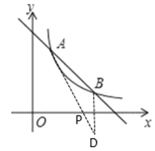
(2)在x軸上找一點P,使PA+PB的值最小,求滿足條件的點P的坐標.

【答案】(1)![]() ,B(2,1);(2)P(
,B(2,1);(2)P(![]() ,0).
,0).
【解析】
(1)由一次函數解析式求出點A的坐標,代入y![]() 中求出反比例函數解析式,再將兩個函數解析式聯立解出點B坐標;
中求出反比例函數解析式,再將兩個函數解析式聯立解出點B坐標;
(2)作點B關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() 并求出直線AD解析式,再求得與
并求出直線AD解析式,再求得與![]() 軸交點
軸交點![]() 的坐標即可得到答案;
的坐標即可得到答案;
(1)解:把點![]() 代人一次函數yx3中,
代人一次函數yx3中,
得![]() ,解得 a=2,
,解得 a=2,
∴A(1,2),將A代入反比例函數![]() ,
,
得![]() ,
,
![]() 反比例函數的表達式為
反比例函數的表達式為![]() ,
,
當![]() 時,
時,
聯立一次函數與反比例函數關系式成方程組,得:
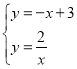 ,解得:
,解得: 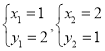 ,
,
∴B(2,1).
(2)如圖,作點B關于![]() 軸的對稱點
軸的對稱點![]() (2,-1),連接與
(2,-1),連接與![]() 軸交于一點即為點
軸交于一點即為點![]() ,此時PA+PB的值最小,
,此時PA+PB的值最小,
設直線AD的關系式為y=kx+b,將點A、D的坐標代入,
得![]() ,解得
,解得![]() ,
,
∴設直線AD的關系式為y=-3x+5,
當y=0時,x=![]() ,
,
∴P(![]() ,0).
,0).


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】列方程解應用題:
中華優秀傳統文化是中華民族的“根”和“魂”,是我們必須世代傳承的文化根脈、文化基因.為傳承優秀傳統文化,某校為各班購進《三國演義》和《水滸傳》連環畫若干套,其中每套《三國演義》連環畫的價格比每套《水滸傳》連環畫的價格貴60元,用4800元購買《水滸傳》連環畫的套數是用3600元購買《三國演義》連環畫套數的2倍,求每套《水滸傳》連環畫的價格.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一條長![]() 米,寬
米,寬![]() 米的矩形草地上修三條小路,小路都等寬,除小路外,草地面積為
米的矩形草地上修三條小路,小路都等寬,除小路外,草地面積為![]() 米2的
米2的![]() 個矩形小塊,則小路的寬度應為( )
個矩形小塊,則小路的寬度應為( )

A. ![]() 米或
米或![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
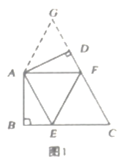
【題目】(1)如圖1,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是
分別是![]() 上的點,且
上的點,且![]() ,探究圖中
,探究圖中![]() 之間的數量關系。小明同學探究此問題的方法是:延長
之間的數量關系。小明同學探究此問題的方法是:延長![]() 到點
到點![]() ,使
,使![]() 。連接
。連接![]() ,先證明
,先證明![]() ,再證明
,再證明![]() ,可得出結論。他的結論應是______________________________________(不寫過程)。
,可得出結論。他的結論應是______________________________________(不寫過程)。
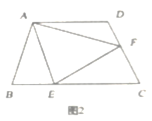
(2)如圖2,若在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是
分別是![]() 上的點,且
上的點,且![]() ,上述結論是否仍然成立,并說明理由。
,上述結論是否仍然成立,并說明理由。
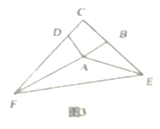
(3)如圖3,已知在四邊形![]() 中,
中,![]() ,
,![]() ,若點
,若點![]() 在
在![]() 的延長線上,點
的延長線上,點![]() 在
在![]() 的延長線上,仍然滿足
的延長線上,仍然滿足![]() ,請寫出
,請寫出![]() 與
與![]() 的數量關系,并給出證明過程。
的數量關系,并給出證明過程。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y =ax2+bx+ c的圖象如圖,有以下結論:①a+b+c<0; ②a-b+c >2;③abc>0;④4a-2b+c <0;⑤c-a>1.其中所有正確結論的序號是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y1=ax2+c與x軸交于A、B兩點,與y軸交于點C,點P在拋物線上,過P(1,﹣3),B(4,0)兩點作直線y2=kx+b.
(1)求a、c的值;
(2)根據圖象直接寫出y1>y2時,x的取值范圍;
(3)在拋物線上是否存在點M,使得S△ABP=5S△ABM,若存在,求出點M的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)水果店張阿姨以每斤2元的價格購進某種水果若干斤,然后以每斤4元的價格出售,每天可售出100斤,通過調查發現,這種水果每斤的售價每降低0.1元,每天可多售出20斤,為保證每天至少售出260斤,張阿姨決定降價銷售.
(1)若將這種水果每斤的售價降低x元,則每天的銷售量是 斤(用含x的代數式表示);
(2)銷售這種水果要想每天盈利300元,張阿姨需將每斤的售價降低多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知在△ABC中,∠ACB=90°,AC=BC=1,點D是AB上任意一點,AE⊥AB,且AE=BD,DE與AC相交于點F.
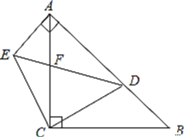
(1)試判斷△CDE的形狀,并說明理由.
(2)是否存在點D,使AE=AF?如果存在,求出此時AD的長,如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在小山的東側A莊,有一熱氣球,由于受西風的影響,以每分鐘35 m的速度沿著與水平方向成75°角的方向飛行,40 min時到達C處,此時氣球上的人發現氣球與山頂P點及小山西側的B莊在一條直線上,同時測得B莊的俯角為30°.又在A莊測得山頂P的仰角為45°,求A莊與B莊的距離及山高(結果保留根號).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com