
【題目】如圖,點E為□ABCD中一點,EA=ED,∠AED=90,點F,G分別為AB,BC上的點,連接DF,AG,AD=AG=DF,且AG⊥DF于點H,連接EG,DG,延長AB,DG相交于點P.
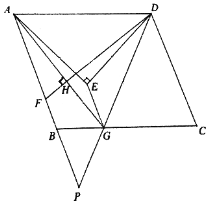
(1)若AH=6,FH=2,求AE的長;
(2)求證:∠P=45;
(3)若DG=2PG,求證:∠AGE=∠EDG.
【答案】(1)![]() ;(2)見詳解;(3)見詳解
;(2)見詳解;(3)見詳解
【解析】
(1)在Rt△ADH中,設AD=DF=x,則DH=x-2,由勾股定理,求出AD的長度,由等腰直角三角形的性質(zhì),即可求出AE的長度;
(2)根據(jù)題意,設∠ADF=2a,則求出∠FAH=![]() ,然后∠ADG=∠AGD=
,然后∠ADG=∠AGD=![]() ,再根據(jù)三角形的外角性質(zhì),即可得到答案;
,再根據(jù)三角形的外角性質(zhì),即可得到答案;
(3)過點A作AM⊥DP于點M,連接EM,EF,根據(jù)等腰直角三角形的判定和性質(zhì),全等三角形的判定和性質(zhì),得到角之間的關系,從而通過等量互換,即可得到結(jié)論成立.
解:(1)∵AG⊥DF于點H,
∴∠AHD=90°,
∵AH=6,FH=2,
在Rt△ADH中,設AD=DF=x,則DH=DF![]() FH=x-2,
FH=x-2,
由勾股定理,得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
即AD=DF=AG=10,
∵EA=ED,∠AED=90,
∴△ADE是等腰直角三角形,
∴AE=DE=![]() ;
;
(2)如圖:

∵∠AED=90,AG⊥DF,
∴∠EAH=∠EDH,
設∠ADF=2a,
∵DA=DF,
則∠AFH=∠DAF=![]() ,
,
∴∠FAH=![]() ,
,
∴∠DAH=![]() ,
,
∵AD=AG,
∴∠ADG=∠AGD=![]() ,
,
∴![]() ;
;
(3)過點A作AM⊥DP于點M,連接EM,EF,如圖:

∵AD=AG,DG=2PG,
∴PG=GM=DM,
∵∠P=45°,
∴△APM是等腰直角三角形,
∴AM=PM=DG,
∵∠ANO=∠DNM,∠AED=∠AMD=90°,
∴∠OAM=∠ODG,
∵AE=DE,AM=DG,
∴△AEM≌△DEG,
∴EM=EG,∠AEM=∠DEG,
∴∠AED+∠DEM=∠DEM+∠MEG,
∴∠MEG=∠AED=90°,
∴△MEG是等腰直角三角形;
∴∠EMG=45°,
∴∠AME=∠EMG=45°,
∴ME是∠AMP的角平分線,
∵AM=PM,
∴ME⊥AP,
∵∠AOH=∠DOE,
∴∠OAH=∠ODE,
∴△AEG≌△DEF(SAS),
∴∠AEG=∠DEF,
∴∠AED+∠AEF=∠AEF+∠FEG,
∴∠FEG=∠AED=90°,
∴∠FEG+∠MEG=180°,
即點F、E、M,三點共線,
∴MF⊥AP,
∵AM平分∠DAG,
∴∠GAM=∠DAM,
∵∠EAN+∠DAM=45°,
∴∠EAN+∠GAM=45°,
∵∠PAG+∠GAM=45°,
∴∠EAN=∠PAG,
∵∠PAG+∠AFH=∠DFE+∠AFH=90°,
∴∠EAN=∠PAG=∠DFE,
∵△AEG≌△DEF,
∴∠AGE=∠DFE=∠EAN,
∵∠EAN=∠EDM,
∴∠AGE=∠EDM,
∴∠AGE=∠EDG.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平行四邊形ABCD的邊AD的延長線上截取DE=AD,F是AE延長線上的一點,連結(jié)BD、CE、BF分別交CE、CD于G、H.
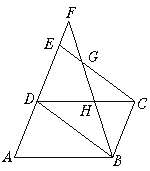
求證:(1)△ABD≌△DCE;
(2)CE∶CG=DF∶AD.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】問題:探究函數(shù)y=x+![]() 的圖象和性質(zhì).
的圖象和性質(zhì).
小華根據(jù)學習函數(shù)的方法和經(jīng)驗,進行了如下探究,下面是小華的探究過程,請補充完整:
(1)函數(shù)的自變量x的取值范圍是:____;
(2)如表是y與x的幾組對應值,請將表格補充完整:
x | … | ﹣3 | ﹣2 | ﹣ | ﹣1 |
|
| 1 |
| 2 | 3 | … |
y | … | ﹣3 | ﹣3 |
| ﹣3 | ﹣4 | 4 |
| 3 | … |
(3)如圖,在平面直角坐標系中描點并畫出此函數(shù)的圖象;
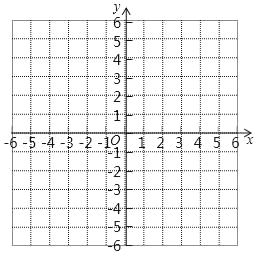
(4)進一步探究:結(jié)合函數(shù)的圖象,寫出此函數(shù)的性質(zhì)(一條即可).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知![]() ,
,![]() 、
、![]() 、
、![]() 的對邊分別是
的對邊分別是![]() 、
、![]() 、
、![]() ,一條直線
,一條直線![]() 與邊
與邊![]() 相交于點
相交于點![]() ,與邊
,與邊![]() 相交于點
相交于點![]() .
.
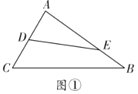
(1)如圖①,若![]() 將
將![]() 分成周長相等的兩部分,求
分成周長相等的兩部分,求![]() 的值;(用
的值;(用![]() 、
、![]() 、
、![]() 表示)
表示)
(2)如圖②,若![]() ,
,![]() ,
,![]() ,
,![]() 將
將![]() 分成周長、面積相等的兩部分,求
分成周長、面積相等的兩部分,求![]() 的值;
的值;
(3)如圖③,若![]() 將
將![]() 分成周長、面積相等的兩部分,且
分成周長、面積相等的兩部分,且![]() ,則
,則![]() 、
、![]() 、
、![]() 滿足什么關系?
滿足什么關系?
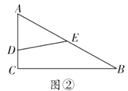
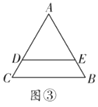
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知△ABC,AB=AC,BD是∠ABC的角平分線,EF是BD的中垂線,且分別交BC于點E,交AB于點F,交BD于點K,連接DE,DF.
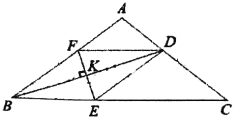
(1)證明:DE//AB;
(2)若CD=3,求四邊形BEDF的周長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
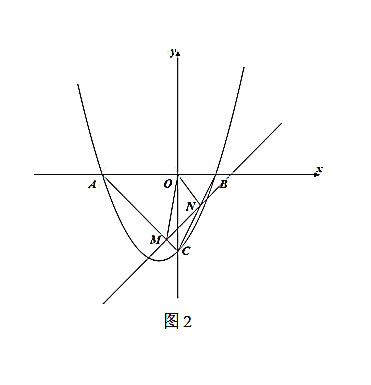
【題目】已知,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,且
,且![]() 點的坐標為
點的坐標為![]() .
.
(1)求該拋物線的解析式.
(2)如圖1,若點![]() 是線段
是線段![]() 上的一動點,過點
上的一動點,過點![]() 作
作![]() ,交
,交![]() 于
于![]() ,連接
,連接![]() ,求
,求![]() 面積的最大值.
面積的最大值.
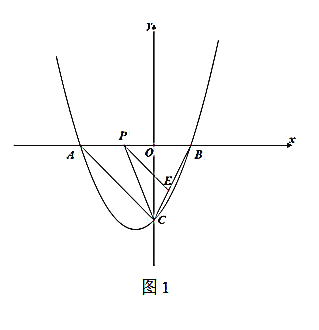
(3)如圖2,若直線![]() 與線段
與線段![]() 交于點
交于點![]() ,與線段
,與線段![]() 交于點
交于點![]() ,是否存在
,是否存在![]() ,
,![]() ,使得
,使得![]() 為直角三角形,若存在,請求出
為直角三角形,若存在,請求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
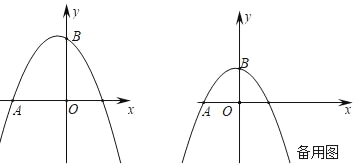
【題目】已知拋物線y=ax2﹣![]() x+c經(jīng)過A(﹣2,0),B(0,2)兩點,動點P,Q同時從原點出發(fā)均以1個單位/秒的速度運動,動點P沿x軸正方向運動,動點Q沿y軸正方向運動,連接PQ,設運動時間為t秒
x+c經(jīng)過A(﹣2,0),B(0,2)兩點,動點P,Q同時從原點出發(fā)均以1個單位/秒的速度運動,動點P沿x軸正方向運動,動點Q沿y軸正方向運動,連接PQ,設運動時間為t秒
(1)求拋物線的解析式;
(2)當BQ=![]() AP時,求t的值;
AP時,求t的值;
(3)隨著點P,Q的運動,拋物線上是否存在點M,使△MPQ為等邊三角形?若存在,請求出t的值及相應點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,一般捕魚船在A處發(fā)出求救信號,位于A處正西方向的B處有一艘救援艇決定前去數(shù)援,但兩船之間有大片暗礁,無法直線到達.救援艇決定馬上調(diào)整方向,先向北偏東![]() 方以每小時30海里的速度航行,同時捕魚船向正北低速航行.30分鐘后,捕魚船到達距離A處
方以每小時30海里的速度航行,同時捕魚船向正北低速航行.30分鐘后,捕魚船到達距離A處![]() 海里的D處,此時救援艇在C處測得D處在南偏東
海里的D處,此時救援艇在C處測得D處在南偏東![]() 的方向上.
的方向上.
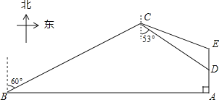
![]() 求C、D兩點的距離;
求C、D兩點的距離;
![]() 捕魚船繼續(xù)低速向北航行,救援艇決定再次調(diào)整航向,沿CE方向前去救援,并且捕魚船和救援艇同達時到E處,若兩船航速不變,求
捕魚船繼續(xù)低速向北航行,救援艇決定再次調(diào)整航向,沿CE方向前去救援,并且捕魚船和救援艇同達時到E處,若兩船航速不變,求![]() 的正弦值.
的正弦值.![]() 參考數(shù)據(jù):
參考數(shù)據(jù):![]() ,
,![]() ,
,![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com