
如圖 ,梯形
,梯形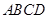 中,
中,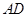 ∥
∥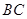 ,
,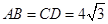 ,
,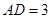 ,
,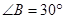 .動點
.動點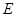 從點
從點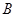 出發,以每秒
出發,以每秒 個單位長度的速度在線段
個單位長度的速度在線段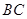 上運動;動點
上運動;動點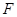 同時從點
同時從點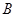 出發,以每秒
出發,以每秒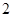 個單位長度的速度在線段
個單位長度的速度在線段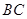 上運動.以
上運動.以 為邊作等邊△
為邊作等邊△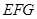 ,與梯形
,與梯形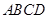 在線段
在線段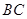 的同側.設點
的同側.設點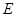 、
、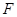 運動時間為
運動時間為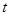 ,當點
,當點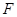 到達
到達 點時,運動結束.
點時,運動結束.
(1)當等邊△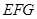 的邊
的邊 恰好經過點
恰好經過點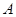 時,求運動時間
時,求運動時間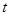 的值;
的值;
(2)在整個運動過程中,設等邊△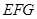 與梯形
與梯形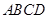 的重合部分面積為
的重合部分面積為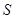 ,請直接寫出
,請直接寫出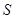 與
與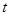 之間的函數關系式和相應的自變量
之間的函數關系式和相應的自變量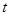 的取值范圍;
的取值范圍;
(3)如圖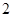 ,當點
,當點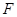 到達
到達 點時,將等邊△
點時,將等邊△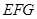 繞點
繞點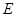 旋轉
旋轉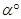 (
(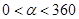 ),
),
直線 分別與直線
分別與直線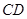 、直線
、直線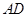 交于點
交于點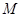 、
、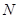 .是否存在這樣的
.是否存在這樣的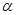 ,使△
,使△ 為等腰三角形?若存在,請求出此時線段
為等腰三角形?若存在,請求出此時線段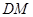 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.
(1)4s(2)
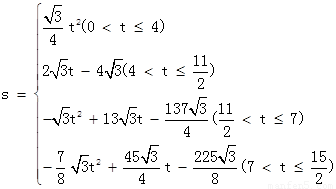
(3)DM的長為: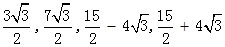
【解析】(1)當EG經過點A時
∴△EGF為等邊△
∴∠AEF=600=∠B+∠BAE
∴∠BAE=∠B=300
∴BE=AE=t=EF
∴此時G與A,重合
∴在Rt△BAF中
2t•cos300=4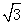
t=4s ......3分
(2)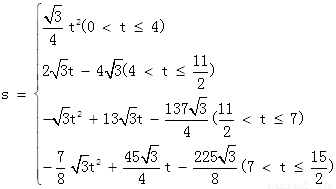 .................8分
.................8分
(3)存在;①當M點在線段CD上時,
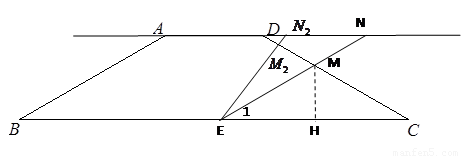
△DMN為等腰三角形
當MD=MN
此時:∠C=∠1=∠N=∠CDN=300
∴ME=MC
作MH⊥CE
EH=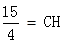
∴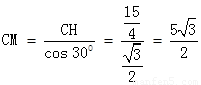
∴DM=
當D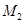 =D
=D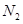 時
時
此時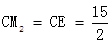
D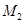 =
=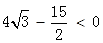 ,不存在
,不存在
當ND=NM時,則∠NDM=∠DMN=300,則M不在線段CD上. ∴舍
②當M在CD延長線上時
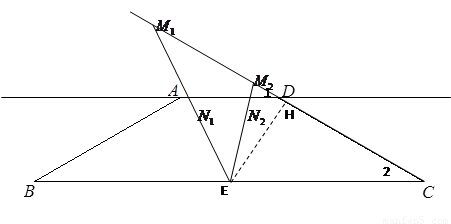
當N1D=N1M1時
∠1=∠M1,又∠1=∠2
∴∠2=∠
∴EM1=CE=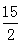
過E作EH⊥CM1
則CM1=2CH=2×CE•cos300
=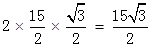
∴DM1=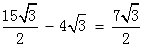
當DM2=DN2時
可知CM2=CE=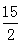
∴DM2=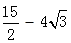
當M3D=M3N時
此時∠M2N2D=∠1=30°
∴此時:∠M3EC=300
則M不在CD延長線上
∴舍去
③當M在DC延長線上時
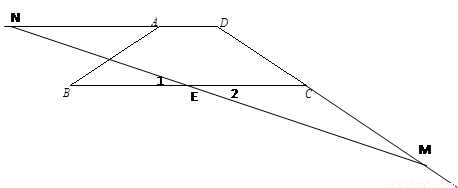
∵∠D為1500
∴△DMN為等腰△時
只有DM=DN
則:∠N=∠1=∠2=∠M
∴CE=CM=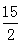
∴DM=4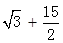
綜上所述DM的長為: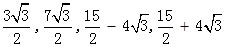 .................12分
.................12分
本試題主要是考查了等邊△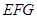 與梯形
與梯形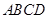 的重合部分面積為
的重合部分面積為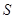 與時間
與時間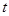 之間的函數關系式,以及利用三角形中的三角函數值得到邊長問題的綜合運用。
之間的函數關系式,以及利用三角形中的三角函數值得到邊長問題的綜合運用。
(1)當EG經過點A時
∴△EGF為等邊△
∴∠AEF=600=∠B+∠BAE
∴∠BAE=∠B=300
∴BE=AE=t=EF
∴此時G與A,重合
∴在Rt△BAF中
2t•cos300=4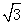
t=4s
(2)根據時間與面積的關系式需要分情況討論得到。
(3)當點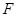 到達
到達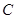 點時,將等邊△
點時,將等邊△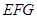 繞點
繞點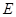 旋轉
旋轉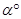 (
(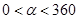 ),
),
直線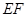 分別與直線
分別與直線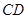 、直線
、直線 交于點
交于點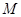 、
、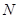 .假設存在這樣的
.假設存在這樣的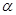 ,使△
,使△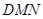 為等腰三角形
為等腰三角形
那么要對點M是在線段CD上,還是在線段CD的延長線上,還是在DC的延長線上三種情況來分析即可。


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
 如圖:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直線MN為梯形ABCD的對稱軸,P為MN上一點,Q為CD上一點,那么PQ+CQ的最小值為
如圖:梯形中ABCD,AD∥BC,AB=CD=5,BC=6,∠C=60°,直線MN為梯形ABCD的對稱軸,P為MN上一點,Q為CD上一點,那么PQ+CQ的最小值為查看答案和解析>>
科目:初中數學 來源: 題型:
 中,
中,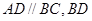 平分
平分 分別為AD、AB中點,點G為BC邊上一點,且
分別為AD、AB中點,點G為BC邊上一點,且
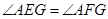 ;
; 時,四邊形
時,四邊形 為平行
為平行 四邊形,并說明理由.
四邊形,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com