
【題目】將一個正整數x的首位數字與末位數字先立方再求和得到一個新數(若x<10,則直接將x立方得到新數),定義為M(x)運算.例如:M(2)=23=8,M(31)=33+13=28,M(102)=13+23=9,規定對某個正整數x進行第一次M(x)運算記作M1(x),第二次M(x)運算記作M2(x),……,第n次M(x)運算記作Mn(x),例如:M1(2)=23=8,M2(2)=83=512,M3(2)=53+23=133.
(1)求M2(3)和M2017(3);
(2)若M5n(3)=520,求正整數n的最小值.
科目:初中數學 來源: 題型:
【題目】 如圖,點E在△DBC的邊DB上,點A在△DBC內部,∠DAE=∠BAC=90°,AD=AE,AB=AC.給出下列結論:①BD=CE;②BC=DC;③∠ABD+∠ECB=45°;④BD⊥CE.其中正確的結論是( )
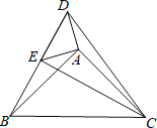
A.①②③④B.②④C.①②③D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“大千故里,文化內江”,我市某中學為傳承大千藝術精神,征集學生書畫作品.王老師從全校20個班中隨機抽取了![]() 4個班,對征集作品進行了數量分析統計,繪制了如下兩幅不完整的統計圖.
4個班,對征集作品進行了數量分析統計,繪制了如下兩幅不完整的統計圖.
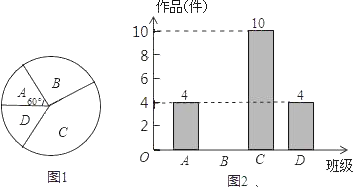
(1)王老師采取的調查方式是 (填“普查”或“抽樣調査”),王老師所調查的4個班共征集到作品 件,并補全條形統計圖;
(2)在扇形統計圖中,表示![]() 班的扇形周心角的度數為 ;
班的扇形周心角的度數為 ;
(3)如果全校參展作品中有4件獲得一等獎,其中有1名作者是男生,3名作者是女生.現要從獲得一等獎的作者中隨機抽取兩人去參加學校的總結表彰座談會,求恰好抽中一男一女的概率.(要求用樹狀圖或列表法寫出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MON=90°,矩形ABCD的頂點A、B分別在邊OM,ON上,當B在邊ON上運動時,A隨之在OM上運動,矩形ABCD的形狀保持不變,其中AB=2,BC=1,運動過程中,點D到點O的最大距離為_____.
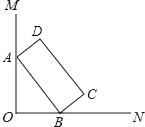
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在河流兩邊有甲、乙兩座山,現在從甲山A處的位置向乙山B處拉電線,已知甲山AC的坡比為15:8.乙山BD的坡比為4:3,甲山上A點到河邊c的距離AC=340米,乙山上B點到河邊D的距離BD=900米,從B處看A處的俯角為26°,則河CD的寬度是(參考值:sin26°=0.4383,tan26°=0.4788,co26°=0.8988)結果精確到0.01)( )

A.177.19米B.188.85米C.192.0米D.258.25米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,以△ABC的邊AB為直徑的⊙O交邊BC于點E,過點E作⊙O的切線交AC于點D,且ED⊥AC.


(1)試判斷△ABC的形狀,并說明理由;
(2)如圖2,若線段AB、DE的延長線交于點F,∠C=75°,CD=![]() ,求⊙O的半徑和BF的長
,求⊙O的半徑和BF的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了參加中考體育測試,甲,乙,丙三位同學進行足球傳球訓練.球從一個人腳下隨機傳到另一個人腳下,且每位傳球人傳球給其余兩人的機會是均等的,由甲開始傳球,共傳三次.
(1)求請用樹狀圖列舉出三次傳球的所有可能情況;
(2)傳球三次后,球回到甲腳下的概率;
(3)三次傳球后,球回到甲腳下的概率大還是傳到丙腳下的概率大?
查看答案和解析>>
科目:初中數學 來源: 題型:
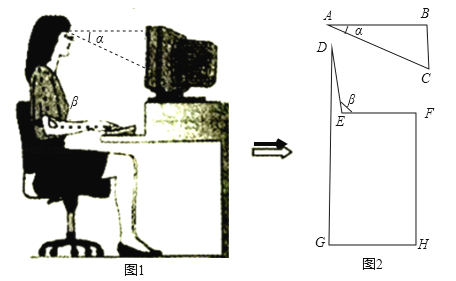
【題目】(2017江西省)如圖1,研究發現,科學使用電腦時,望向熒光屏幕畫面的“視線角”α約為20°,而當手指接觸鍵盤時,肘部形成的“手肘角”β約為100°.圖2是其側面簡化示意圖,其中視線AB水平,且與屏幕BC垂直.
(1)若屏幕上下寬BC=20cm,科學使用電腦時,求眼睛與屏幕的最短距離AB的長;
(2)若肩膀到水平地面的距離DG=100cm,上臂DE=30cm,下臂EF水平放置在鍵盤上,其到地面的距離FH=72cm.請判斷此時β是否符合科學要求的100°?
(參考數據:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有結果精確到個位)
,所有結果精確到個位)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一個直角三角形紙片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分別是AC、AB邊上點,連接EF.
(1)圖①,若將紙片ACB的一角沿EF折疊,折疊后點A落在AB邊上的點D處,且使S四邊形ECBF=3S△EDF,求AE的長;
(2)如圖②,若將紙片ACB的一角沿EF折疊,折疊后點A落在BC邊上的點M處,且使MF∥CA.
①試判斷四邊形AEMF的形狀,并證明你的結論;
②求EF的長;
(3)如圖③,若FE的延長線與BC的延長線交于點N,CN=1,CE=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com