
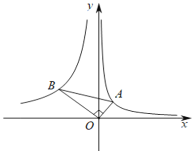
【題目】如圖,Rt△AOB中,∠AOB=90°,![]() ,頂點A在反比例函數(shù)
,頂點A在反比例函數(shù)![]() 則點B所在的反比例函數(shù)解析式為_________.
則點B所在的反比例函數(shù)解析式為_________.
【答案】![]()
【解析】
分別過點A、B作x軸的垂線,根據(jù)∠AOB=90°,容易證得△BOD∽△OAC,設(shè)點A的坐標,由![]() 可得相似比為
可得相似比為![]() ,求得點B的坐標即可求出反比例函數(shù)的解析式.
,求得點B的坐標即可求出反比例函數(shù)的解析式.
過點A作AC⊥x軸,過點B作BD⊥x軸,分別交x軸于點C、點D,如圖,
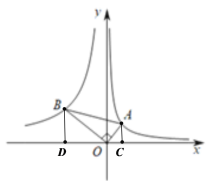
設(shè)A點坐標為![]() ,
,
則OC=a,AC=![]() ,
,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∵AC⊥OC,BD⊥OD,
∴∠BDO=∠ACO=90°,
∴∠AOC+∠OAC=90°,
∴∠BOD=∠OAC
∴△BOD∽△OAC,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴點B的坐標為![]() ,
,
設(shè)過點B的反比例函數(shù)的解析式為![]() ,代入點B的坐標可得,
,代入點B的坐標可得,
![]() ,
,
∴點B所在的反比例函數(shù)解析式為![]() ,
,
故答案為:![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】過直線外一點且與這條直線相切的圓稱為這個點和這條直線的點線圓.特別地,半徑最小的點線圓稱為這個點和這條直線的最小點線圓.
在平面直角坐標系![]() 中,點
中,點![]() .
.
(1)已知點![]() ,
,![]() ,
,![]() ,分別以
,分別以![]() ,
,![]() 為圓心,1為半徑作
為圓心,1為半徑作![]() ,
,![]() ,以
,以![]() 為圓心,2為半徑作
為圓心,2為半徑作![]() ,其中是點
,其中是點![]() 和
和![]() 軸的點線圓的是________;
軸的點線圓的是________;
(2)記點![]() 和
和![]() 軸的點線圓為
軸的點線圓為![]() ,如果
,如果![]() 與直線
與直線![]() 沒有公共點,求
沒有公共點,求![]() 的半徑
的半徑![]() 的取值范圍;
的取值范圍;
(3)直接寫岀點![]() 和直線
和直線![]() 的最小點線圓的圓心的橫坐標
的最小點線圓的圓心的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】有這樣一個問題:探究函數(shù)![]() 的圖象與性質(zhì).
的圖象與性質(zhì).
小菲根據(jù)學習函數(shù)的經(jīng)驗,對函數(shù)![]() 的圖象與性質(zhì)進行了探究.
的圖象與性質(zhì)進行了探究.
下面是小菲的探究過程,請補充完整:
(1)函數(shù)![]() 的自變量
的自變量![]() 的取值范圍是___________________.
的取值范圍是___________________.
(2)下表是![]() 與
與![]() 的幾組對應(yīng)值.
的幾組對應(yīng)值.
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | … |
| … |
|
|
|
|
|
|
| 2 |
|
| … |
表中![]() 的值為____________________________.
的值為____________________________.
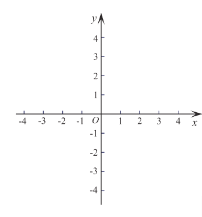
(3)如下圖,在平面直角坐標系![]() 中,描出補全后的表中各組對應(yīng)值所對應(yīng)的點,并畫出該函數(shù)的圖象;
中,描出補全后的表中各組對應(yīng)值所對應(yīng)的點,并畫出該函數(shù)的圖象;
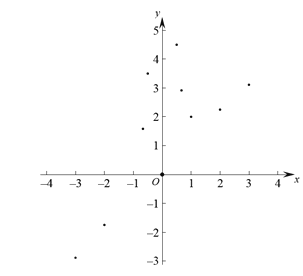
(4)根據(jù)畫出的函數(shù)圖象,寫出:
①![]() 時,對應(yīng)的函數(shù)值
時,對應(yīng)的函數(shù)值![]() 約為__________________(結(jié)果保留一位小數(shù));
約為__________________(結(jié)果保留一位小數(shù));
②該函數(shù)的一條性質(zhì):________________________________________________________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
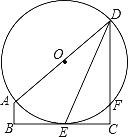
【題目】如圖,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD為直徑的⊙O與BC相切于點E,交CD于點F,連接DE.
(1)證明:DE平分∠ADC;
(2)已知AD=4,設(shè)CD的長為x(2<x<4).
①當x=2.5時,求弦DE的長度;
②當x為何值時,DFFC的值最大?最大值是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知關(guān)于x的二次函數(shù)y=ax2﹣4ax+a+1(a>0)
(1)若二次函數(shù)的圖象與x軸有交點,求a的取值范圍;
(2)若P(m,n)和Q(5,b)是拋物線上兩點,且n>b,求實數(shù)m的取值范圍;
(3)當m≤x≤m+2時,求y的最小值(用含a、m的代數(shù)式表示).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某賓館有50個房間供游客居住,當每個房間定價120元時,房間會全部住滿,當每個房間每天的定價每增加10元時,就會有一個房間空閑。如果游客居住房間,賓館需對每個房間每天支出20元的各種費用,設(shè)每個房間定價增加10 x元(x為整數(shù))。
(1)(2分)直接寫出每天游客居住的房間數(shù)量y與x的函數(shù)關(guān)系式。
(2)(4分)設(shè)賓館每天的利潤為W元,當每間房價定價為多少元時,賓館每天所獲利潤最大,最大利潤是多少?
(3)(4分)某日,賓館了解當天的住宿的情況,得到以下信息:①當日所獲利潤不低于5000元,②賓館為游客居住的房間共支出費用沒有超過600元,③每個房間剛好住滿2人。問:這天賓館入住的游客人數(shù)最少有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(2010河南20題)為鼓勵學生參與體育鍛煉,學校計劃拿出不超過1600元的資金再購買一批籃球和排球.已知籃球和排球的單價比為![]() ,單價和為80元.
,單價和為80元.
(1)籃球和排球的單價分別是多少元?
(2)若要求購買的籃球和排球的總數(shù)量是36個,且購買的籃球的數(shù)量多于25個,有哪幾種購買方案?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
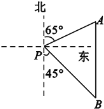
【題目】如圖,一艘海輪位于燈塔P的北偏東65°方向,距離燈塔80海里的A處,它沿正南方向航行一段時間后,到達位于燈塔P的南偏東45°方向上的B處,則這時海輪所在的B處距離燈塔P的距離是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面內(nèi),對于給定的![]() ,如果存在一個半圓或優(yōu)弧與
,如果存在一個半圓或優(yōu)弧與![]() 的兩邊相切,且該弧上的所有點都在
的兩邊相切,且該弧上的所有點都在![]() 的內(nèi)部或邊上,則稱這樣的弧為
的內(nèi)部或邊上,則稱這樣的弧為![]() 的內(nèi)切弧.當內(nèi)切弧的半徑最大時,稱該內(nèi)切弧為
的內(nèi)切弧.當內(nèi)切弧的半徑最大時,稱該內(nèi)切弧為![]() 的完美內(nèi)切弧.(注:弧的半徑指該弧所在圓的半徑)
的完美內(nèi)切弧.(注:弧的半徑指該弧所在圓的半徑)
在平面直角坐標系![]() 中,
中,![]() .
.
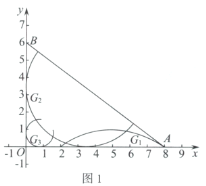
(1)如圖1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的內(nèi)切弧的是____________;
的內(nèi)切弧的是____________;
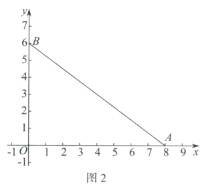
(2)如圖2,若弧G為![]() 的內(nèi)切弧,且弧G與邊
的內(nèi)切弧,且弧G與邊![]() 相切,求弧G的半徑的最大值;
相切,求弧G的半徑的最大值;
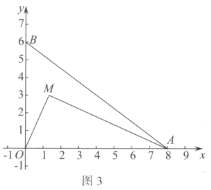
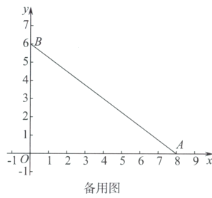
(3)如圖3,動點![]() ,連接
,連接![]() .
.
①直接寫出![]() 的完美內(nèi)切弧的半徑的最大值;
的完美內(nèi)切弧的半徑的最大值;
②記①中得到的半徑最大時的完美內(nèi)切弧為弧T.點P為弧T上的一個動點,過點P作x軸的垂線,分別交x軸和直線![]() 于點D,E,點F為線段
于點D,E,點F為線段![]() 的中點,直接寫出線段
的中點,直接寫出線段![]() 長度的取值范圍.
長度的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com