
【題目】(1)閱讀理解:如圖1,在![]() 中,若
中,若![]() ,
,![]() .求
.求![]() 邊上的中線
邊上的中線![]() 的取值范圍.小聰同學(xué)是這樣思考的:延長(zhǎng)
的取值范圍.小聰同學(xué)是這樣思考的:延長(zhǎng)![]() 至
至![]() ,使
,使![]() ,連結(jié)
,連結(jié)![]() .利用全等將邊
.利用全等將邊![]() 轉(zhuǎn)化到
轉(zhuǎn)化到![]() ,在
,在![]() 中利用三角形三邊關(guān)系即可求出中線
中利用三角形三邊關(guān)系即可求出中線![]() 的取值范圍.在這個(gè)過(guò)程中小聰同學(xué)證三角形全等用到的判定方法是__________;中線
的取值范圍.在這個(gè)過(guò)程中小聰同學(xué)證三角形全等用到的判定方法是__________;中線![]() 的取值范圍是__________.
的取值范圍是__________.
(2)問(wèn)題解決:如圖2,在![]() 中,點(diǎn)
中,點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在
在![]() 邊上,點(diǎn)
邊上,點(diǎn)![]() 在
在![]() 邊上,若
邊上,若![]() .求證:
.求證:![]() .
.
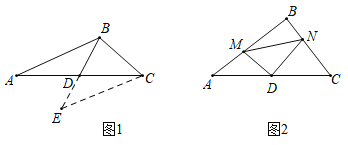
【答案】(1)![]() ,
,![]() ;(2)見(jiàn)解析.
;(2)見(jiàn)解析.
【解析】
(1)延長(zhǎng)![]() 至
至![]() ,使
,使![]() ,連
,連![]() ,先證明
,先證明![]() ,得到
,得到![]() ,再由三角形的三邊關(guān)系即可解答.
,再由三角形的三邊關(guān)系即可解答.
(2)連![]() ,并延長(zhǎng)
,并延長(zhǎng)![]() 至
至![]() ,使
,使![]() ,連
,連![]() ,延長(zhǎng)
,延長(zhǎng)![]() 交
交![]() 于
于![]() ,連
,連![]() ,由(1)先證明
,由(1)先證明![]() ,得到
,得到![]() ,
,![]() ,根據(jù)
,根據(jù)![]() ,得到
,得到![]() 是線段
是線段![]() 的垂直平分線,所以
的垂直平分線,所以![]() ,然后三角形三邊關(guān)系即可解答.
,然后三角形三邊關(guān)系即可解答.
(1)解:如圖,延長(zhǎng)![]() 至
至![]() ,使
,使![]() ,連
,連![]() ,
,
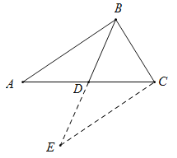
∵![]() 是
是![]() 邊上的中線,
邊上的中線,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,由三角形的三邊關(guān)系得:
中,由三角形的三邊關(guān)系得:![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ;
;
故答案為:![]() ,
,![]() ;
;
(2)如圖,連![]() ,并延長(zhǎng)
,并延長(zhǎng)![]() 至
至![]() ,使
,使![]() ,連
,連![]() ,延長(zhǎng)
,延長(zhǎng)![]() 交
交![]() 于
于![]() ,連
,連![]() ,
,

由(1)可知![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]() ,
,
在![]() 中,由三邊關(guān)系得
中,由三邊關(guān)系得![]() ,
,
∴![]() .
.


 同步練習(xí)強(qiáng)化拓展系列答案
同步練習(xí)強(qiáng)化拓展系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】感恩節(jié)即將來(lái)臨,小王調(diào)查了初三年級(jí)部分同學(xué)在感恩節(jié)當(dāng)天將以何種方式對(duì)幫助過(guò)自己的人表達(dá)感謝,他將調(diào)查結(jié)果分為如下四類(lèi):A類(lèi)﹣﹣當(dāng)面表示感謝、B類(lèi)﹣﹣打電話表示感謝、C類(lèi)﹣﹣發(fā)短信表示感謝、D類(lèi)﹣﹣寫(xiě)書(shū)信表示感謝.他將調(diào)查結(jié)果繪制成了如圖所示的扇形統(tǒng)計(jì)圖和條形統(tǒng)計(jì)圖.請(qǐng)你根據(jù)圖中提供的信息完成下列各題:
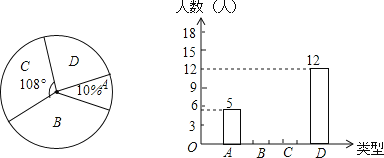
(1)補(bǔ)全條形統(tǒng)計(jì)圖;
(2)在A類(lèi)的同學(xué)中,有4人來(lái)自同一班級(jí),其中有2人主持過(guò)班會(huì).現(xiàn)準(zhǔn)備從他們4人中隨機(jī)抽出兩位同學(xué)主持感恩節(jié)主題班會(huì)課,請(qǐng)用樹(shù)狀圖或列表法求抽出1人主持過(guò)班會(huì)而另一人沒(méi)主持過(guò)班會(huì)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,則點(diǎn)A2 019的坐標(biāo)為____________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在Rt△ABC中,∠C=90°,P是BC邊上不同于B、C的一動(dòng)點(diǎn),過(guò)P作PQ⊥AB,垂足為Q,連接AP.

(1)試說(shuō)明不論點(diǎn)P在BC邊上何處時(shí),都有△PBQ與△ABC相似;
(2)若Rt△AQP≌Rt△ACP≌Rt△BQP,求tanB的值;
(3)已知AC=3,BC=4,當(dāng)BP為何值時(shí),△AQP面積最大,并求出最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】統(tǒng)計(jì)七年級(jí)部分同學(xué)的跳高測(cè)試成績(jī),得到如下頻率直方圖(每組含前一個(gè)邊界值,不含后一個(gè)邊界值).

(1)參加測(cè)試的總?cè)藬?shù)是多少人?
(2)組距為多少?
(3)跳高成績(jī)?cè)?/span>![]() (含
(含![]() )以上的有多少人?占總?cè)藬?shù)的百分之幾?
)以上的有多少人?占總?cè)藬?shù)的百分之幾?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊的中點(diǎn),點(diǎn)
邊的中點(diǎn),點(diǎn)![]() 是
是![]() 邊上一動(dòng)點(diǎn)(不與點(diǎn)
邊上一動(dòng)點(diǎn)(不與點(diǎn)![]() 重合),延長(zhǎng)
重合),延長(zhǎng)![]() 交射線
交射線![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,
,![]() .
.

(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)填空:
①當(dāng)![]() 的值為_______時(shí),四邊形
的值為_______時(shí),四邊形![]() 是矩形;
是矩形;
②當(dāng)![]() 的值為______時(shí),四邊形
的值為______時(shí),四邊形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
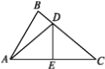
【題目】如圖,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于點(diǎn)D,交AC于點(diǎn)E.
(1)求∠BAD的度數(shù);
(2)若AB=10,BC=12,求△ABD的周長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四邊形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如圖,若α=90°,根據(jù)教材中一個(gè)重要性質(zhì)直接可得 DA=CD,這個(gè)性質(zhì)是 ;

(2)問(wèn)題解決:如圖,求證:AD=CD;

(3)問(wèn)題拓展:如圖,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求證:BD+AD=BC.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com