
【題目】如圖,△ABC是等腰直角三角形,∠BCA=90°,BC=AC,直角頂點C在y軸上,銳角頂點A在x軸上.
(1)如圖①,若點C的坐標是(0,-1),點A的坐標是(-3,0),求B點的坐標;
(2)如圖②,若x軸恰好平分∠BAC,BC與x軸交于點D,過點B作BE⊥x軸于E,問AD與BE有怎樣的數量關系,并說明理由;
(3)如圖③,直角邊AC在兩坐標軸上滑動,使點B在第四象限內,過B點作BF⊥x軸于F,在滑動的過程中,猜想OC、BF、OA之間的關系,并證明你的結論.
【答案】(1)(1,2);(2)AD=2BE,理由見解析;(3)OC=BF+OA,證明見解析;
【解析】
(1)如圖①,過B作BG⊥y軸于G,證明△AOC≌△CGB(AAS),得AO=CG=3,OC=BG=1,表示點B的坐標;
(2)如圖②,延長BE、AC交于H,證明△AEB≌△AEH(ASA),得BE=EH,即BH=2BE,再證明△ACD≌△BCH(ASA),可得結論;
(3)如圖③,過C作CM⊥BF,交FB的延長線于M,證明△AOC≌△BMC(AAS),四邊形OCMF為矩形,根據線段的和可得結論.
(1)如圖①,過B作BG⊥y軸于G,
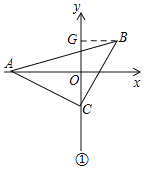
∵點C的坐標是(0,-1),點A的坐標是(-3,0),
∴OC=1,OA=3,
∵∠BCA=90°,
∴∠ACO+∠BCG=90°,
∵∠BCG+∠CBG=90°,
∴∠ACO=∠CBG,
∵AC=BC,∠AOC=∠BGC=90°,
∴△AOC≌△CGB(AAS),
∴AO=CG=3,OC=BG=1,
∴OG=3-1=2,
∴B(1,2);
(2)如圖②,AD=2BE,
理由是:延長BE、AC交于H,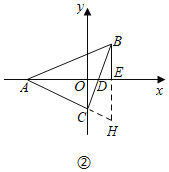
∵BE⊥x軸,
∴∠AEB=∠AEH=90°,
∵AE平分∠BAC,
∴∠CAD=∠BAD,
∵AE=AE,
∴△AEB≌△AEH(ASA),
∴BE=EH,即BH=2BE,
∵∠ACD=∠BED=90°,∠ADC=∠BDE,
∴∠CAD=∠CBH,
∵AC=BC,∠ACD=∠BCH=90°,
∴△ACD≌△BCH(ASA),
∴AD=BH=2BE;
(3)OC=BF+OA,
理由是:如圖③,過C作CM⊥BF,交FB的延長線于M,
同理可得:△AOC≌△BMC(AAS),
∴AO=BM,OC=CM,
∵∠COF=∠OFM=∠M=90°,
∴四邊形OCMF為矩形,
∴FM=OC,
∴FM=BF+BM,
∴OC=BF+OA.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:初中數學 來源: 題型:
【題目】錦潭社區計劃對某區域進行綠化,經投標,由甲、乙兩個工程隊一起來完成,已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的![]() 倍,并且在獨立完成面積為
倍,并且在獨立完成面積為![]() 區域的綠化時,甲隊比乙隊少用
區域的綠化時,甲隊比乙隊少用![]() 天.
天.
(1)求甲、乙兩工程隊每天各能完成的綠化面積;
(2)若計劃綠化的區域面積是![]() ,甲隊每天綠化費用是
,甲隊每天綠化費用是![]() 萬元,乙隊每天綠化費用為
萬元,乙隊每天綠化費用為![]() 萬元.
萬元.
①當甲、乙各施工幾天,既能剛好完成綠化任務,又能使總費用恰好為![]() 萬元;
萬元;
②按要求甲隊至少施工![]() 天,乙隊至多施工
天,乙隊至多施工![]() 天,當甲乙各施工幾天,既能剛好完成綠化任務,又使得總費用最少(施工天數不能是小數)并求最少總費用.
天,當甲乙各施工幾天,既能剛好完成綠化任務,又使得總費用最少(施工天數不能是小數)并求最少總費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系![]() 中,已知點
中,已知點![]() 的坐標
的坐標![]() ,過
,過![]() 點作
點作![]() 軸,垂足為點
軸,垂足為點![]() ,過點
,過點![]() 作直線
作直線![]() 軸,點
軸,點![]() 從點
從點![]() 出發在
出發在![]() 軸上沿著軸的正方向運動.
軸上沿著軸的正方向運動.

(1)當點![]() 運動到點
運動到點![]() 處,過點
處,過點![]() 作
作![]() 的垂線交直線
的垂線交直線![]() 于點
于點![]() ,證明
,證明![]() ,并求此時點
,并求此時點![]() 的坐標;
的坐標;
(2)點![]() 是直線
是直線![]() 上的動點,問是否存在點
上的動點,問是否存在點![]() ,使得以
,使得以![]() 為頂點的三角形和
為頂點的三角形和![]() 全等,若存在求點
全等,若存在求點![]() 的坐標以及此時對應的點
的坐標以及此時對應的點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,AE平分∠BAD交BC邊于E,EF⊥AE交CD邊于F,延長BA到點G,使AG=CF,連接GF,若BC=7,DF=3,AE=![]() ,則GF的長為__________
,則GF的長為__________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2011年11月28日,為擴大內需,國務院決定在全國實施“家電下鄉“政策.第一批列入家電下鄉的產品為彩電、冰箱、洗衣機和手機四種產品.某縣一家家電商場,今年一季度對以上四種產品的銷售情況進行了統計,繪制了如下的統計圖,根據圖中信息求:

(1)彩電占四種家電下鄉產品的百分比;
(2)該商場一季度冰箱銷售的數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉鎮風力資源豐富,為了實現低碳環保,該鄉鎮決定開展風力發電,打算購買10臺風力發電機組.現有A,B兩種型號機組,其中A型機組價格為12萬元/臺,月均發電量為2.4萬kw.h;B型機組價格為10萬元/臺,月均發電量為2萬kw.h.經預算該鄉鎮用于購買風力發電機組的資金不高于105萬元.
(1)請你為該鄉鎮設計幾種購買方案;
(2)如果該鄉鎮用電量不低于20.4萬kw.h/月,為了節省資金,應選擇那種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示.在△ABC中,內角∠BAC與外角∠CBE的平分線相交于點P,BE=BC,PB與CE交于點H,PG∥AD交BC于F,交AB于G,連接CP.下列結論:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正確的有( )

A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列括號內填理由:已知:如圖,AC∥DE,CD、EF分別為∠ACB、∠DEB的平分線.
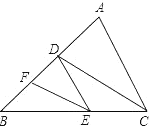
求證:CD∥EF
證明:∵AC∥DE〔已知)
∴ = ( )
∵CD、EF分別為∠ACB、∠DEB的平分線.(已知)
![]() ,
,![]() ( )
( )
∴∠DCB=∠FEB
∴CD∥EF( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,CD平分∠ACB交AB于點D,AE∥DC交BC的延長線于點E,已知∠BAC=32°,求∠E的度數為_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com