
某商品的進(jìn)價(jià)為每件40元,售價(jià)為每件50元,每個月可賣出210件;如果每件商品的售價(jià)每上漲1元,則每個月少賣10件(每件售價(jià)不能高于65元).
設(shè)每件商品的售價(jià)上漲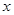 元(
元(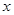 為正整數(shù)),每個月的銷售利潤為
為正整數(shù)),每個月的銷售利潤為 元.
元.
(1)求 與
與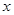 的函數(shù)關(guān)系式并直接寫出自變量
的函數(shù)關(guān)系式并直接寫出自變量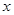 的取值范圍;
的取值范圍;
(2)每件商品的售價(jià)定為多少元時,每個月可獲得最大利潤?最大的月利潤是多少元?
(3)每件商品的售價(jià)定為多少元時,每個月的利潤恰為2200元?根據(jù)以上結(jié)論,請你直接寫出售價(jià)在什么范圍時,每個月的利潤不低于2200元?
(1)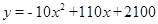 (0<x≤15且x為整數(shù));(2)55或56,2400;
(0<x≤15且x為整數(shù));(2)55或56,2400;
(3) ,
, ,不低于51元且不高于60元且為整數(shù).
,不低于51元且不高于60元且為整數(shù).
解析試題分析:(1)由銷售單價(jià)每漲1元,就會少售出10件,得
(0<x≤15且x為整數(shù));
(2)把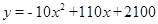 進(jìn)行配方即可求出最大值,即最大利潤.
進(jìn)行配方即可求出最大值,即最大利潤.
(3)當(dāng)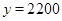 時,
時,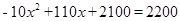 ,解得:
,解得: ,
, .
.
當(dāng) 時,
時, ,當(dāng)
,當(dāng) 時,
時, .
.
當(dāng)售價(jià)定為每件51或60元,每個月的利潤為2200元.
試題解析:(1) (
( 且
且 為整數(shù));
為整數(shù));
(2)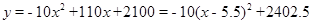 .
.
∵a=-10<0,
∴當(dāng)x=5.5時,y有最大值2402.5.
∵0<x≤15且x為整數(shù),
∴當(dāng)x=5時,50+x=55,y=2400(元),當(dāng)x=6時,50+6=56,y=2400(元)
∴當(dāng)售價(jià)定為每件55或56元,每個月的利潤最大,最大的月利潤是2400元.
(3)當(dāng)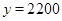 時,
時,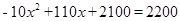 ,解得:
,解得: ,
, .
.
∴當(dāng) 時,
時, ,當(dāng)
,當(dāng) 時,
時, .
.
∴當(dāng)售價(jià)定為每件51或60元,每個月的利潤為2200元.
∴當(dāng)售價(jià)不低于51或60元,每個月的利潤為2200元.
∴當(dāng)售價(jià)不低于51元且不高于60元且為整數(shù)時,每個月的利潤不低于2200元(或當(dāng)售價(jià)分別為51,52,53,54,55,56,57,58,59,60元時,每個月的利潤不低于2200元).
考點(diǎn):1.二次函數(shù)的應(yīng)用;2.一元二次方程的應(yīng)用.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知拋物線y=ax2+bx+c經(jīng)過A(-1,0)、B(3,0)、C(0,3)三點(diǎn),直線l是拋物線的對稱軸.
(1)求拋物線的函數(shù)關(guān)系式;
(2)設(shè)點(diǎn)P是直線l上的一個動點(diǎn),當(dāng)△PAC的周長最小時,求點(diǎn)P的坐標(biāo),并求出此時的周長;
(3)在直線l上是否存在點(diǎn)M,使△MAC為直角三角形?若存在,請寫出所有符合條件的點(diǎn)M的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,拋物線 與y軸交于點(diǎn)A,拋物線上的一點(diǎn)P在第四象限,連接AP與x軸交于點(diǎn)C,
與y軸交于點(diǎn)A,拋物線上的一點(diǎn)P在第四象限,連接AP與x軸交于點(diǎn)C, ,且S△AOC=1,過點(diǎn)P作PB⊥y軸于點(diǎn)B.
,且S△AOC=1,過點(diǎn)P作PB⊥y軸于點(diǎn)B.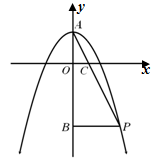
(1)求BP的長;
(2)求拋物線與x軸的交點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在邊長為24cm的正方形紙片ABCD上,剪去圖中陰影部分的四個全等的等腰直角三角形,再沿圖中的虛線折起,折成一個長方體形狀的包裝盒(A、B、C、D四個頂點(diǎn)正好重合于上底面上一點(diǎn))。已知E、F在AB邊上,是被剪去的一個等腰直角三角形斜邊的兩個端點(diǎn),設(shè)AE=BF=x(cm).
(1)若折成的包裝盒恰好是個正方體,試求這個包裝盒的體積V;
(2)某廣告商要求包裝盒的表面(不含下底面)面積S最大,試問x應(yīng)取何值?S最大值是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
為了落實(shí)國務(wù)院的指示精神,某地方政府出臺了一系列“三農(nóng)”優(yōu)惠政策,使農(nóng)民收入大幅度增加.某農(nóng)戶生產(chǎn)經(jīng)銷一種農(nóng)產(chǎn)品,已知這種產(chǎn)品的成本價(jià)為每千克20元,市場調(diào)查發(fā)現(xiàn),該產(chǎn)品每天的銷售量y(千克)與銷售價(jià)x(元/千克)有如下關(guān)系:y=﹣2x+80.設(shè)這種產(chǎn)品每天的銷售利潤為w元.
(1)求w與x之間的函數(shù)關(guān)系式.
(2)該產(chǎn)品銷售價(jià)定為每千克多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果物價(jià)部門規(guī)定這種產(chǎn)品的銷售價(jià)不高于每千克28元,該農(nóng)戶想要每天獲得150元的銷售利潤,銷售價(jià)應(yīng)定為每千克多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知拋物線 過兩點(diǎn)(m,0)、(n,0),且
過兩點(diǎn)(m,0)、(n,0),且 ,拋物線于雙曲線
,拋物線于雙曲線 (x>0)的交點(diǎn)為(1,d).
(x>0)的交點(diǎn)為(1,d).
(1)求拋物線與雙曲線的解析式;
(2)已知點(diǎn) 都在雙曲線
都在雙曲線 (x>0)上,它們的橫坐標(biāo)分別為
(x>0)上,它們的橫坐標(biāo)分別為 ,O為坐標(biāo)原點(diǎn),記
,O為坐標(biāo)原點(diǎn),記 ,點(diǎn)Q在雙曲線
,點(diǎn)Q在雙曲線 (x<0)上,過Q作QM⊥y軸于M,記
(x<0)上,過Q作QM⊥y軸于M,記 。
。
求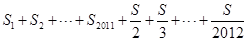 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
一座橋如圖,橋下水面寬度AB是20米,高CD是4米.要使高為3米的船通過,則其寬度須不超過多少米.
(1)如圖1,若把橋看做是拋物線的一部分,建立如圖坐標(biāo)系.
①求拋物線的解析式;
②要使高為3米的船通過,則其寬度須不超過多少米?
(2)如圖2,若把橋看做是圓的一部分.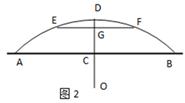
①求圓的半徑;
②要使高為3米的船通過,則其寬度須不超過多少米?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知拋物線y=ax2+bx+3(a≠0)經(jīng)過A(3,0),B(4,1)兩點(diǎn),且與y軸交于點(diǎn)C.
(1)求拋物線y=ax2+bx+3(a≠0)的函數(shù)關(guān)系式及點(diǎn)C的坐標(biāo);
(2)如圖(1),連接AB,在題(1)中的拋物線上是否存在點(diǎn)P,使△PAB是以AB為直角邊的直角三角形?若存在,求出點(diǎn)P的坐標(biāo);若不存在,請說明理由;
(3)如圖(2),連接AC,E為線段AC上任意一點(diǎn)(不與A、C重合)經(jīng)過A、E、O三點(diǎn)的圓交直線AB于點(diǎn)F,當(dāng)△OEF的面積取得最小值時,求點(diǎn)E的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com