

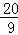 s;(2)t=
s;(2)t=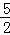 s時,S取得最大值為
s時,S取得最大值為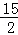 cm2;(3)不存在
cm2;(3)不存在 ,即
,即 ,解出即可;
,解出即可;  ,即
,即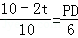 ,解得PD=6﹣
,解得PD=6﹣ t,即可得到S關于t的二次函數,根據二次函數的性質即可求得結果;
t,即可得到S關于t的二次函數,根據二次函數的性質即可求得結果; S△ABC=12.由(2)可知,S△AQP=﹣
S△ABC=12.由(2)可知,S△AQP=﹣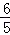 t2+6t,則有﹣
t2+6t,則有﹣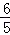 t2+6t=12,根據此方程無解,即可作出判斷.
t2+6t=12,根據此方程無解,即可作出判斷.

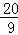
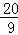 s時,PQ∥BC
s時,PQ∥BC 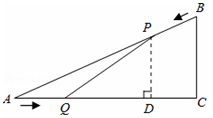
 ,
,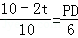 ,
, t
t  ×AQ×PD=
×AQ×PD= ×2t×(6﹣
×2t×(6﹣ t)
t) t2+6t=﹣
t2+6t=﹣ (t﹣
(t﹣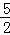 )2+
)2+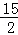 ,
,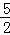 s時,S取得最大值,最大值為
s時,S取得最大值,最大值為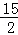 cm2
cm2  S△ABC=12.
S△ABC=12.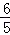 t2+6t,
t2+6t,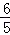 t2+6t=12,
t2+6t=12,

科目:初中數學 來源:不詳 題型:解答題
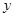 (萬件)與銷售單價
(萬件)與銷售單價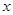 (元)之間的關系可以近似地看作一次函數
(元)之間的關系可以近似地看作一次函數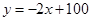 .(利潤=售價-制造成本)
.(利潤=售價-制造成本)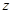 (萬元)與銷售單價
(萬元)與銷售單價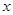 (元)之間的函數關系式;
(元)之間的函數關系式;查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
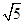 cm/s的速度運動,在折線DE-EB上以1cm/s的速度運動.當點P與點A不重合時,過點P作PQ⊥AC于點Q,以PQ為邊作正方形PQMN,使點M在直線AQ上.設點P的運動時間為t(s).
cm/s的速度運動,在折線DE-EB上以1cm/s的速度運動.當點P與點A不重合時,過點P作PQ⊥AC于點Q,以PQ為邊作正方形PQMN,使點M在直線AQ上.設點P的運動時間為t(s).
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
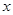 軸兩交點間的距離為8,(1)試求該拋物線的關系式;
軸兩交點間的距離為8,(1)試求該拋物線的關系式;查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
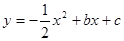 的圖象經過這兩點
的圖象經過這兩點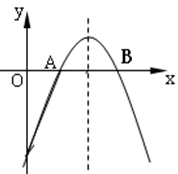
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com