
【題目】已知二次函數y=ax2+bx+c的圖象經過點(2,-5),頂點坐標為(-1,4),直線l的解析式為y=2x+m.
(1)求拋物線的解析式;
(2)若拋物線與直線l有兩個公共點,求![]() 的取值范圍;
的取值范圍;
(3)若直線l與拋物線只有一個公共點P,求點P的坐標;
(4)設拋物線與![]() 軸的交點分別為A、B,求在(3)的條件下△PAB的面積.
軸的交點分別為A、B,求在(3)的條件下△PAB的面積.
【答案】(1)y=-x2-2x+3;(2)當m<7時,拋物線與直線l有兩個公共點;(3)點P的坐標為(-2,3);(4)SPAB=6.
【解析】
(1)由拋物線頂點坐標可得二次函數y=a(x+1)2+4,將點(2,-5)代入,即可得到拋物線的解析式,
(2)由拋物線的解析式及直線l的解析式聯立,利用△即可求出拋物線與直線l有兩個公共點m的取值范圍,
(3)由拋物線的解析式及直線l的解析式聯立,利用△=0時求出m的值,再聯立即可求出點P的坐標,
(4)拋物線的解析式求出AB的長,利用S△PAB=![]() ABP縱坐標,即可求出△PAB的面積.
ABP縱坐標,即可求出△PAB的面積.
解:(1)∵拋物線頂點坐標為(-1,4),
∴它的解析式為y=a(x+1)2+4,將點(2,-5)代入,得a=-1.
∴拋物線的解析式為:y=-x2-2x+3.
(2)由![]() ,
,
得x2-4x+m-3=0,
∴△=16-4(m-3)=-4m+28.
當-4m+28>0時,解得m<7.
即當m<7時,拋物線與直線l有兩個公共點.
(3)由(2)知:當拋物線與直線l只有一個公共點時,m=7,
由![]()
解得![]() ,
,
即點P的坐標為(-2,3).
(4)∵拋物線的解析式為:y=-x2-2x+3.拋物線與x軸的交點分別為A、B,
∴令0=-x2-2x+3,得x1=-3,x2=1,
∴AB=4,
∴S△PAB=![]() ABP縱坐標=
ABP縱坐標=![]() ×4×3=6.
×4×3=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】(2017重慶A卷第11題)如圖,小王在長江邊某瞭望臺D處,測得江面上的漁船A的俯角為40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡長BC=10米,則此時AB的長約為( )(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中數學 來源: 題型:
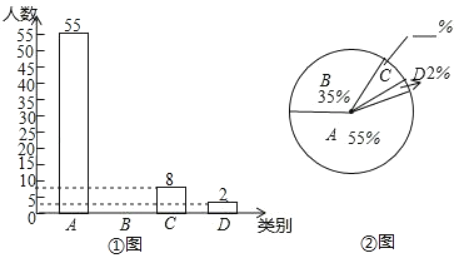
【題目】我省某地區為了了解2017年初中畢業生畢業去向,對部分九年級學生進行了抽樣調查,就九年級學生畢業后的四種去向:A.讀重點高中;B.讀職業高中;C.直接進入社會就業;D.其他(如出國等)進行數據統計,并繪制了兩幅不完整的統計圖(如①圖,如②圖)
(1)該地區共調查了_____名九年級學生;
(2)將兩幅統計圖中不完整的部分補充完整;
(3)若該地區2017年初中畢業生共有4000人,請估計該地區今年初中畢業生中讀重點高中的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c的圖象的一部分,對稱軸是直線x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是拋物線上的兩點,則y1<y2.
上述4個判斷中,正確的是( )

A.①② B.①④ C.①③④ D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
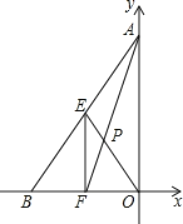
【題目】如圖,在平面直角坐標系中,O為坐標原點,點A,B的坐標分別為(0,4),(﹣3,0),E為AB的中點,EF∥AO交OB于點F,AF與EO交于點P,則EP的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
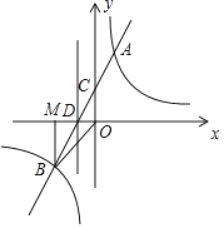
【題目】如圖,一次函數y=mx+n(m≠0)的圖象與反比例函數y=![]() (k≠0)的圖象交于第一、三象限內的A,B兩點,與y軸交于點C,過點B作BM⊥x軸,垂足為點M,BM=OM=2,點A的縱坐標為4.
(k≠0)的圖象交于第一、三象限內的A,B兩點,與y軸交于點C,過點B作BM⊥x軸,垂足為點M,BM=OM=2,點A的縱坐標為4.
(1)求該反比例函數和一次函數的表達式;
(2)直線AB交x軸于點D,過點D作直線l⊥x軸,如果直線l上存在點P,坐標平面內存在點Q.使四邊形OPAQ是矩形,求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極配合我市文明城市創建,居委會組織了兩個檢查組,分別對轄區內新華園、清華園、德才園、御花園四個小區“垃圾分類”和“違規停車”的情況進行抽查,每個檢查組隨機抽取轄區內的一個小區進行檢查.
(1)“違規停車”檢查組抽到新華園小區的概率為_____;
(2)求兩個組恰好同時抽到御花園小區進行檢查的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學舉行“校園朗讀者”朗誦大賽,高、初中部根據初賽成績,各選出5名選手組成初中代表隊和高中代表隊參加學校決賽,兩個隊各選出的5名選手的決賽成績如圖所示.
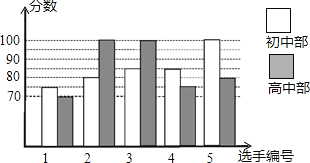
(1)根據圖示填寫表格;
平均分(分) | 中位數(分) | 眾數(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(2)結合兩隊成績的平均數和中位數, 隊的決賽成績較好;
(3)已知高中代表隊決賽成績的方差為160,計算初中代表隊決賽成績的方差,并判斷哪一個代表隊選手成績較為穩定.(方差公式:S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2]
)2]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com