【題目】計算題
（1）若3a=6，9b=2，求32a+4b的值；
（2）已知xy=8，x﹣y=2，求代數(shù)式 
x3y﹣x2y2+ xy3的值．
【答案】
（1）解：∵3a=6，9b=2，
∴32a+4b=32a×34b=（3a）2×（32b）2=36×4=144
（2）解：∵xy=8，x﹣y=2，
∴原式= 
xy（x2﹣2xy+y2）
= xy（x﹣y）2
= ×8×22
=16
【解析】（1）同底數(shù)冪的加法，指數(shù)不變，系數(shù)相加；同底數(shù)冪的乘法，底數(shù)不變，指數(shù)相加；同底數(shù)冪的除法，底數(shù)不變，指數(shù)相減；冪的乘方，底數(shù)不變，指數(shù)相乘；計算即可.
【考點精析】本題主要考查了同底數(shù)冪的乘法的相關知識點，需要掌握同底數(shù)冪的乘法法則aman=am+n(m,n都是正數(shù))才能正確解答此題．
科目：初中數(shù)學 來源： 題型：
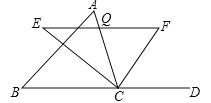
【題目】如圖，在△ABC中，點O是邊AC上一個動點，過點O作直線EF∥BC分別交∠ACB、外角∠ACD的平分線于點E、F．
（1）若CE=8，CF=6，求OC的長；
（2）連接AE、AF．問：當點O在邊AC上運動到什么位置時，四邊形AECF是矩形？并說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
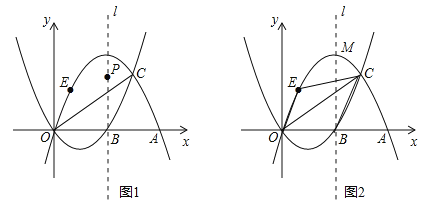
【題目】如圖1，拋物線
：
與
：
相交于點O、C，與分別交x軸于點B、A，且B為線段AO的中點．
（1）求
的值；
（2）若OC⊥AC，求△OAC的面積；
（3）拋物線C2的對稱軸為l，頂點為M，在（2）的條件下：
①點P為拋物線C2對稱軸l上一動點，當△PAC的周長最小時，求點P的坐標；
②如圖2，點E在拋物線C2上點O與點M之間運動，四邊形OBCE的面積是否存在最大值？若存在，求出面積的最大值和點E的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，點A，B，C在一次函數(shù) 
的圖像上，它們的橫坐標依次為-1，1，2，分別過這些點作 
軸與 
軸的垂線，則圖中陰影部分的面積之和是（ ）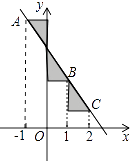
A.3
B.4.5
C.
D.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com