
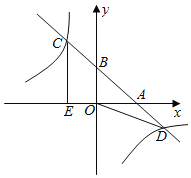
【題目】如圖,直線y=﹣x+b與x、y軸的正半軸交于點A,B,與雙曲線y=﹣![]() 交于點C(點C在第二象限內),點D,過點C作CE⊥x軸于點E,記四邊形OBCE的面積為S1,△OBD的面積為S2,若
交于點C(點C在第二象限內),點D,過點C作CE⊥x軸于點E,記四邊形OBCE的面積為S1,△OBD的面積為S2,若![]() =
=![]() ,則b的值為_____.
,則b的值為_____.
【答案】3
【解析】
根據雙曲線的對稱性得到BC=AD,設BC=AD=a,用a表示出點C和得D的坐標,根據梯形面積公式、三角形面積公式求出a、b的關系,根據反比例函數圖象上點的坐標特征列出方程,解方程求出b.
解:由題意點B的坐標為(0,b),點A的坐標為(b,0),
∴OA=OB=b,
∵直線y=﹣x+b關于直線y=x對稱,反比例函數y=﹣![]() 關于y=x對稱,
關于y=x對稱,
∴BC=AD,
設BC=AD=a,則C(﹣![]() a,b+
a,b+![]() a),D(b+
a),D(b+![]() a,﹣
a,﹣![]() a),
a),
∵![]() =
=![]() ,
,
∴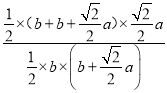 =
=![]() ,
,
整理得,12a2+17![]() ab﹣14b2=0,
ab﹣14b2=0,
解得,a1=![]() b,a2=﹣b(舍去),
b,a2=﹣b(舍去),
則D(![]() b,﹣
b,﹣![]() b),
b),
∴![]() b×(﹣
b×(﹣![]() b)=﹣4,
b)=﹣4,
解得,b1=3,b2=﹣3(舍去),
∴b=3,
故答案為:3.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某年級共有 150 名女生,為了解該年級女生實心球成績(單位:米)和一分鐘仰臥起坐成績(單位:個)的情況,從中隨機抽取 30 名女生進行測試,獲得了她們的相關成績,并對數據進行了整理,下面給出了部分信息.
a.實心球成績的頻數分布如表所示:

b.實心球成績在 7.0≤x<7.4 這一組的是:7.0,7.0,7.0,7.1,7.1,7.1,7.2,7.2,7.3,7.3
c.一分鐘仰臥起坐成績如圖所示:
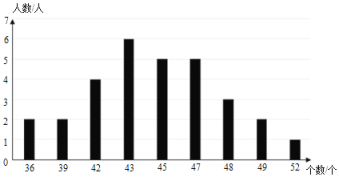
根據以上信息,回答下列問題:
(1)①表中 m 的值為 ;②一分鐘仰臥起坐成績的中位數為 ;
(2)若實心球成績達到 7.2 米及以上時,成績記為優秀.
①請估計全年級女生實心球成績達到優秀的人數;
②該年級某班體育委員將本班在這次抽樣測試中被抽取的 8 名女生的兩項成績的數據抄錄如表所示:

其中有 3 名女生的一分鐘仰臥起坐成績未抄錄完整,但老師說這 8 名女生中恰好有4 人兩項測試成績都達到了優秀,于是體育委員推測女生 E 的一分鐘仰臥起坐成績達到了優秀,你是否同意體育委員的說法? (填“是”或“否”).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年的新冠疫情爆發,使很多農作物積壓沒法正常銷售。為解決農民的困難,我市某食品加工公司主動分兩次采購了一批竹筍, 第一次花費40萬元,第二次花費60萬元。已知第一次采購時每百千克竹筍的價格比去年的平均價格上漲了500元,第二次采購時每百千克竹筍的價格比去年的平均價格下降了500元,第二次的采購數量是第一次采購數量的兩倍.
(1)試問去年每百千克竹筍的平均價格是多少元;
(2)該公司可將竹筍加工成筍干或罐頭(濕筍),若單獨加工成筍干,每天可加工8百千克竹筍,每百千克竹筍獲利1000元; 若單獨加工成罐頭,每天可加工12百千克竹筍,每百千克竹筍獲利600元,由于市場需要,所有采購的竹筍必需在30天內加工完畢,且加工筍干的竹筍數量不少于加工罐頭的竹筍數量的一半,為獲得最大利潤,應將多少百千克竹筍加工成筍干?最大利潤為多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
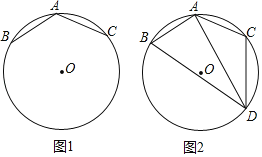
【題目】如圖1,已知A、B、C是⊙O上的三點,AB=AC,∠BAC=120°.
(1)求證:⊙O的半徑R=AB;
(2)如圖2,若點D是∠BAC所對弧上的一動點,連接DA,DB,DC.
①探究DA,DB,DC三者之間的數量關系,并說明理由;
②若AB=3,點C'與C關于AD對稱,連接C'D,點E是C'D的中點,當點D從點B運動到點C時,求點E的運動路徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘數學家畢達哥拉斯認為:“一切平面圖形中最美的是圓”.請研究如下美麗的圓.如圖,線段AB是⊙O的直徑,延長AB至點C,使BC=OB,點E是線段OB的中點,DE⊥AB交⊙O于點D,點P是⊙O上一動點(不與點A,B重合),連接CD,PE,PC.
(1)求證:CD是⊙O的切線;
(2)小明在研究的過程中發現![]() 是一個確定的值.回答這個確定的值是多少?并對小明發現的結論加以證明.
是一個確定的值.回答這個確定的值是多少?并對小明發現的結論加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
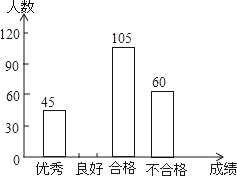
【題目】為了解今年初三學生的數學學習情況,某校對上學期的數學成績作了統計分析,繪制得到如下圖表.請結合圖表所給出的信息解答下列問題:
成績 | 頻數 | 頻率 |
優秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)該校初三學生共有多少人?
(2)求表中a,b,c的值,并補全條形統計圖.
(3)初三(一)班數學老師準備從成績優秀的甲、乙、丙、丁四名同學中任意抽取兩名同學做學習經驗介紹,求恰好選中甲、乙兩位同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】教育未來指數是為了評估教育系統在培養學生如何應對快速多變的未來社會方面所呈現的效果.現對教育未來指數得分前35名的國家和地區的有關數據進行收集、整理、描述和分析后,給出了部分信息.
a.教育未來指數得分的頻數分布直方圖(數據分成7組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
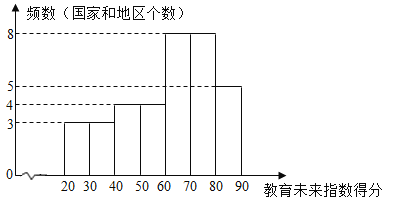
b.教育未來指數得分在![]() 這一組的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
這一組的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
c.35個國家和地區的人均國內生產總值和教育未來指數得分情況統計圖如下:
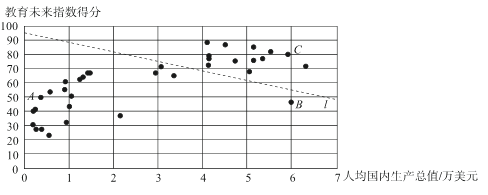
d.中國和中國香港的教育未來指數得分分別為32.9和68.5.
(以上數據來源于《國際統計年鑒(2018)》和國際在線網)
根據以上信息,回答下列問題:
(1)中國香港的教育未來指數得分排名世界第______;
(2)在35個國家和地區的人均國內生產總值和教育未來指數得分情況統計圖中,包括中國香港在內的少數幾個國家和地區所對應的點位于虛線l的上方,請在圖中用“○”畫出代表中國香港的點;
(3)在教育未來指數得分比中國高的國家和地區中,人均國內生產總值的最大值約為_____萬美元;(結果保留一位小數)
(4)下列推斷合理的是__________.(只填序號即可)
①相較于點![]() 所代表的國家和地區,中國的教育未來指數得分還有一定差距,“十三五”規劃提出“教育優先發展,教育強則國家強”的任務,進一步提高國家教育水平;
所代表的國家和地區,中國的教育未來指數得分還有一定差距,“十三五”規劃提出“教育優先發展,教育強則國家強”的任務,進一步提高國家教育水平;
②相較于點![]() 所代表的國家和地區,中國的人均國內生產總值還有一定差距,中國提出“決勝全面建成小康社會”的奮斗目標,進一步提高人均國內生產總值.
所代表的國家和地區,中國的人均國內生產總值還有一定差距,中國提出“決勝全面建成小康社會”的奮斗目標,進一步提高人均國內生產總值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小文設計的“過圓外一點作圓的切線”的作圖過程.已知:![]() 和圓外一點
和圓外一點![]() .求作:過點
.求作:過點![]() 的
的![]() 的切線.作法:①連接
的切線.作法:①連接![]() ;②以
;②以![]() 為直徑作
為直徑作![]() ,交
,交![]() 于點
于點![]() ,
,![]() ;③作直線
;③作直線![]() ,
,![]() ;所以直線
;所以直線![]() ,
,![]() 為
為![]() 的切線.
的切線.
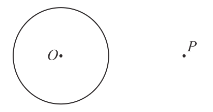
根據小文設計的作圖過程,完成下面的證明.
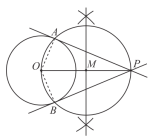
證明:連接![]() ,
,![]() .
.
∵![]() 為
為![]() 的直徑,
的直徑,
∴![]() =∠________=________
=∠________=________
(________)(填推理的依據).
∴![]() ,________
,________![]() .
.
∵![]() ,
,![]() 為
為
∴直線![]() ,
,![]() 為
為![]() 的切線(________)(填推理的依據).
的切線(________)(填推理的依據).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,動點![]() 在平面直角坐標系
在平面直角坐標系![]() 中,按圖中箭頭所示方向運動,第1次從原點運動到點(1,2),第2次接著運動到點(2,0),第3次接著運動到點(3,1),第4次接著運動到點(4,0),……,按這樣的運動規律,經過第27次運動后,動點
中,按圖中箭頭所示方向運動,第1次從原點運動到點(1,2),第2次接著運動到點(2,0),第3次接著運動到點(3,1),第4次接著運動到點(4,0),……,按這樣的運動規律,經過第27次運動后,動點![]() 的坐標是( )
的坐標是( )
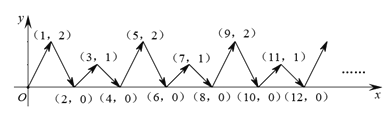
A.(26,0)B.(26,1)C.(27,1)D.(27,2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com