【題目】如果一個多邊形的各邊都相等，且各內角也都相等，那么這個多邊形就叫做正多邊形．如圖，就是一組正多邊形，觀察每個正多邊形中∠α的變化情況： 
（1）將下面的表格補充完整：
（2）根據規律，是否存在一個正多邊形，其中的∠α=21°？若存在，請求出n的值，若不存在，請說明理由．
正多邊形邊數 | 3 | 4 | 5 | 6 | … | n |
∠α的度數 | 60° | … |
【答案】
（1）解：n=4時，360°÷4=90°，∠α=90°÷2=45°，
n=5時，360°÷5=72°，∠α=72°÷2=36°，
n=6時，360°÷6=60°，∠α=60°÷2=30°，
邊數為n時，∠α= 
× 
= 
（2）45°；36°；30°；
【解析】解：（2）假設存在一個正多邊形，其中的∠α=21°，
則 =21°，
解得n= 
（不是整數），
所以，不存在一個正多邊形使∠α=21°．
【考點精析】根據題目的已知條件，利用多邊形內角與外角的相關知識可以得到問題的答案，需要掌握多邊形的內角和定理：n邊形的內角和等于（n-2）180°.多邊形的外角和定理：任意多邊形的外角和等于360°．
小學教材全測系列答案
小學數學口算題卡脫口而出系列答案
優秀生應用題卡口算天天練系列答案科目：初中數學 來源： 題型：
【題目】小明在課外學習時遇到這樣一個問題：
定義：如果二次函數
是常數與
是常數）滿足
，則稱這兩個函數互為“旋轉函數”．
求函數
的 “旋轉函數”．
小明是這樣思考的：由
函數可知a1=-1，b1=3，c1=-3，根據a1+a2=0，b1=b2，c1+c2=0求出a2,b2,c2，就能確定這個函數的“旋轉函數”．
請參考小明的方法解決下面的問題：
（1）寫出函數
的“旋轉函數”；
（2）若函數
與
互為“旋轉函數”，求（m+n）2017的值；
（3）已知函數
的圖象與
軸交于A、B兩點，與y軸交于點C，點A、B、C關于原點的對稱點分別是A1、B1、C1，試證明經過點A1、B1、C1的二次函數與函數
互為“旋轉函數”．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場為了迎接"6.1兒童節"，以調低價格的方式促銷n個不同的玩具，調整后的單價y(元)與調整前的單價x（元）滿足一次函數關系，如下表：
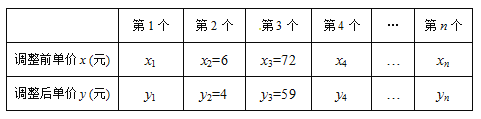
當這些玩具調整后的單價都大于2元時，解答下列問題：
(1) y與x的函數關系式為 ，x的取值范圍為 ；
(2) 某個玩具調整前單價是108元，顧客購買這個玩具省了 元；
(3) 這n個玩具調整前、后的平均單價分別為
(元)、
(元），猜想
與
的關系式，并寫出推導過程.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 數據3，4，4，7，3的眾數是4
B. 數據0，1，2，5，a的中位數是2
C. 一組數據的眾數和中位數不可能相等
D. 數據0，5，－7，－5，7的中位數和平均數都是0
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算：
（1）﹣82+72÷36
（2）2 
× 
÷（﹣9+19）
（3）（ ﹣ 
+ 
）×（﹣36）
（4）1 × 
﹣（﹣ ）×2 +（﹣ ）÷1 
（5）﹣13﹣（1﹣0.5）× 
×[2﹣（﹣3）2]．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
