
認真閱讀下面關于三角形內、外角平分線所夾的 探究片段,完成所提出的問題.
探究片段,完成所提出的問題.
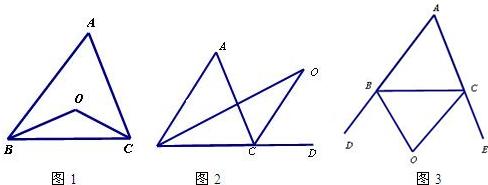
探究1:如圖1,在△ABC中,O是∠ABC與∠ACB的平分線BO和CO的交點,通過分析發現∠BOC=90°+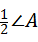 ,理由如下:
,理由如下:
∵ BO和CO分別是∠ABC和∠ACB的角平分線,
∴ .
.
∴ 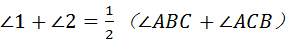 .
.
又∵∠ABC+∠ACB=180°﹣∠A,
∴ 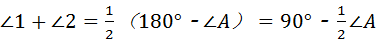 .
.
∴ ∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ∠A)
∠A)
=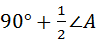 .
.
探究2:如圖2中,O是 ∠ABC與外角∠ACD的平分線BO和CO的交點,試分析∠BOC與∠A有怎樣的關系?請說明理由.
∠ABC與外角∠ACD的平分線BO和CO的交點,試分析∠BOC與∠A有怎樣的關系?請說明理由.
探究3:如圖3中,O是外角∠DBC與外角∠ECB的平分線BO和CO的交點,則∠BOC與∠A有怎樣的關系?(只寫結論,不需證明)
結論: .
|
分析:(1)根據提供的信息,根據三角形的一個外角等于與它不相鄰的兩個內角的和,用∠A與∠1表示出∠2,再利用∠O與∠1表示出∠2,然后整理即可得到∠BOC與∠O的關系;
(2)根據三角形的一個外角等于與它不相鄰的兩個內角的和以及角平分線的定義表示出∠OBC與∠OCB,然后再根據三角形的內角和定理列式整理即可得解.
解:(1)探究2結論:∠BOC= ∠A,
∠A,
理由如下:
∵ BO和CO分別是∠ABC和∠ACD的角平分線,
∴∠1= ∠ABC,∠2=
∠ABC,∠2= ∠ACD,
∠ACD,
又∵∠ACD是△ABC的 一外角,
一外角,
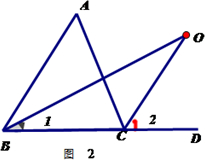 ∴∠ACD=∠A+∠ABC,
∴∠ACD=∠A+∠ABC,
∴∠2= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠1,
∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1= ∠A+∠1﹣∠1=
∠A+∠1﹣∠1= ∠A;
∠A;
(2)探究3:∠OBC= (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB= (∠A+∠ABC),
(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣∠OCB,
=180°﹣ (∠A+∠ACB)﹣
(∠A+∠ACB)﹣ (∠A+∠ABC),
(∠A+∠ABC),
=180°﹣ ∠A﹣
∠A﹣ (∠A+∠ABC+∠ACB),
(∠A+∠ABC+∠ACB),
結論∠BOC=90°﹣ ∠A.
∠A.


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:
2012年我市某縣籌備20周年縣慶,園林部門決定利用現有的3 490盆甲種花卉和2 950盆乙種花卉搭配 兩種園藝造型共50個擺放在迎賓大道兩側,已知搭配一個
兩種園藝造型共50個擺放在迎賓大道兩側,已知搭配一個 種造型需甲種花卉80盆,乙種花卉40盆,搭配一個
種造型需甲種花卉80盆,乙種花卉40盆,搭配一個 種造型需甲種花卉50盆,乙種花卉90盆.
種造型需甲種花卉50盆,乙種花卉90盆.
(1)某校九年級(1)班課外活動小組承接了這個園藝造型搭配方案的設計,問符合題意的搭配方案有幾種?請你幫助設計出來.
(2)若搭配一個 種造型的成本是800元,搭配一個
種造型的成本是800元,搭配一個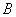 種造型的成本是960元,試說明(1)中哪種方案成本最低?最低成本是多少元?
種造型的成本是960元,試說明(1)中哪種方案成本最低?最低成本是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com