
題目列表(包括答案和解析)
已知 .
.
(1)求 的單調區間;
的單調區間;
(2)證明:當 時,
時, 恒成立;
恒成立;
(3)任取兩個不相等的正數 ,且
,且 ,若存在
,若存在 使
使 成立,證明:
成立,證明: .
.
【解析】(1)g(x)=lnx+ ,
, =
=
 (1’)
(1’)
當k 0時,
0時, >0,所以函數g(x)的增區間為(0,+
>0,所以函數g(x)的增區間為(0,+ ),無減區間;
),無減區間;
當k>0時, >0,得x>k;
>0,得x>k; <0,得0<x<k∴增區間(k,+
<0,得0<x<k∴增區間(k,+ )減區間為(0,k)(3’)
)減區間為(0,k)(3’)
(2)設h(x)=xlnx-2x+e(x 1)令
1)令 = lnx-1=0得x=e, 當x變化時,h(x),
= lnx-1=0得x=e, 當x變化時,h(x), 的變化情況如表
的變化情況如表
|
x |
1 |
(1,e) |
e |
(e,+ |
|
|
|
- |
0 |
+ |
|
h(x) |
e-2 |
|
0 |
↗ |
所以h(x) 0, ∴f(x)
0, ∴f(x) 2x-e
(5’)
2x-e
(5’)
設G(x)=lnx- (x
(x 1)
1)  =
= =
=
 0,當且僅當x=1時,
0,當且僅當x=1時, =0所以G(x) 為減函數, 所以G(x)
=0所以G(x) 為減函數, 所以G(x)  G(1)=0, 所以lnx-
G(1)=0, 所以lnx-
 0所以xlnx
0所以xlnx
 (x
(x 1)成立,所以f(x)
1)成立,所以f(x) 
 ,綜上,當x
,綜上,當x 1時, 2x-e
1時, 2x-e f(x)
f(x)
 恒成立.
恒成立.
(3) ∵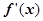 =lnx+1∴lnx0+1=
=lnx+1∴lnx0+1= =
= ∴lnx0=
∴lnx0=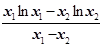 -1
∴lnx0 –lnx
-1
∴lnx0 –lnx =
= -1–lnx
-1–lnx =
= =
= =
= (10’) 設H(t)=lnt+1-t(0<t<1),
(10’) 設H(t)=lnt+1-t(0<t<1),
 =
= =
=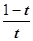 >0(0<t<1), 所以H(t) 在(0,1)上是增函數,并且H(t)在t=1處有意義, 所以H(t)
<H(1)=0∵
>0(0<t<1), 所以H(t) 在(0,1)上是增函數,并且H(t)在t=1處有意義, 所以H(t)
<H(1)=0∵ ∴
∴ =
=
∴lnx0 –lnx >0, ∴x0 >x
>0, ∴x0 >x
(本小題滿分9分)以下是用二分法求方程 的一個近似解(精確度為0.1)的不完整的過程,請補充完整。
的一個近似解(精確度為0.1)的不完整的過程,請補充完整。
|
區間 |
中點 |
|
區間長度 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
解:設函數 ,其圖象在
,其圖象在 上是連續不斷的,且
上是連續不斷的,且 在
在 上是單調遞______(增或減)。先求
上是單調遞______(增或減)。先求 _______,
_______, ______,
______, ____________。
____________。
所以 在區間____________內存在零點
在區間____________內存在零點 ,再填上表:
,再填上表:
下結論:_______________________________。
(可參考條件: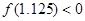 ,
, ;符號填+、-)
;符號填+、-)
 的一個近似解(精確度為0.1)的不完整的過程,請補充完整。
的一個近似解(精確度為0.1)的不完整的過程,請補充完整。| 區間 | 中點 |  符號 符號 | 區間長度 |
| | | | |
| | | | |
| | | | |
| | | | |
| | | | |
 ,其圖象在
,其圖象在 上是連續不斷的,且
上是連續不斷的,且 在
在 上是單調遞______(增或減)。先求
上是單調遞______(增或減)。先求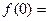 _______,
_______, ______,
______, ____________。
____________。 在區間____________內存在零點
在區間____________內存在零點 ,再填上表:
,再填上表: ,
, ;符號填+、-)
;符號填+、-)(本小題滿分9分)
以下是用二分法求方程![]() 的一個近似解(精確度為0.1)的不完整的過程,請補充完整。
的一個近似解(精確度為0.1)的不完整的過程,請補充完整。
| 區間 | 中點 |
| 區間長度 |
解:設函數![]() ,
,
其圖象在上是連續不
斷的,且![]() 在上是
在上是
單調遞______(增或減)。
先求![]() _______,
_______,
![]() ______,
______,
![]() ____________。
____________。
所以![]() 在區間____________內存在零點
在區間____________內存在零點![]() ,再填上表:
,再填上表:
下結論:_______________________________。
(可參考條件:![]() ,
,![]() ;符號填+、-)
;符號填+、-)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com