
題目列表(包括答案和解析)
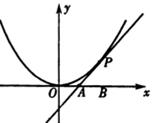
如圖,已知直線l與拋物線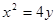 相切于點P(2,1),且與x軸交于點A,O為坐標原點,定點B的坐標為(2,0).
相切于點P(2,1),且與x軸交于點A,O為坐標原點,定點B的坐標為(2,0).
(I) 若動點M滿足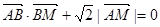 ,求點M的軌跡C;
,求點M的軌跡C;
(II)若過點B的直線l′(斜率不等于零)與(I)中的軌跡C交于不同的兩點E、F(E在B、F之間),試求△OBE與△OBF面積之比的取值范圍
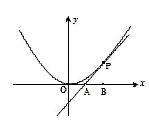
如圖,已知直線![]() 與拋物線
與拋物線![]() 相切于點P(2, 1),且與
相切于點P(2, 1),且與![]() 軸交于點A,定點B的坐標為(2, 0) .
軸交于點A,定點B的坐標為(2, 0) .
(I)若動點M滿足![]() ,求點M的軌跡C;
,求點M的軌跡C;
(II)若過點B的直線![]() (斜率不等于零)與(I)中的軌跡C交于不同的兩點E、F(E在B、F之間),試求
(斜率不等于零)與(I)中的軌跡C交于不同的兩點E、F(E在B、F之間),試求![]() OBE與
OBE與![]() OBF面積之比的取值范圍.
OBF面積之比的取值范圍.
(滿分12分)直線l 與拋物線y2 = 4x 交于兩點A、B,O 為原點,且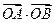 = -4.
= -4.
(I) 求證:直線l 恒過一定點;
(II) 若 4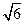 ≤| AB | ≤
≤| AB | ≤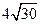 ,求直線l 的
,求直線l 的 斜率k 的取值范圍;
斜率k 的取值范圍;
(Ⅲ) 設拋物線的焦點為F,∠AFB = θ,試問θ 角 能否
能否 等于120°?若能,求出相應的直線l 的方程;若不能,請說明理由.
等于120°?若能,求出相應的直線l 的方程;若不能,請說明理由.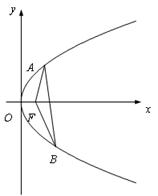
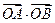 = -4.
= -4.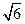 ≤| AB | ≤
≤| AB | ≤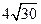 ,求直線l 的
,求直線l 的 斜率k 的取值范圍;
斜率k 的取值范圍; 能否
能否 等于120°?若能,求出相應的直線l 的方程;若不能,請說明理由.
等于120°?若能,求出相應的直線l 的方程;若不能,請說明理由.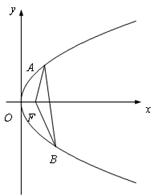
(本小題滿分12分)
已知點A(0,1)、B(0,-1),P為一個動點,且直線PA、PB的斜率之積為![]()
(I)求動點P的軌跡C的方程;
(II)設Q(2,0),過點(-1,0)的直線![]() 交C于M、N兩點,
交C于M、N兩點,![]() 的面積記為S,若對滿足條件的任意直線
的面積記為S,若對滿足條件的任意直線![]() ,不等式
,不等式![]() 的最小值。
的最小值。
一、BCBBA BCDCB DB
二.填空題:本大題共4小題,每小題5分,共20分
13
 14 ..4 15.
14 ..4 15.  16. (2,3)
16. (2,3)
三、解答題(本大題共6小題,共70分,解答應寫出文字說明、證明過程或演算步驟)
17. (本大題共10分)
解:由于y=2x是增函數, 等價于
等價于
 . ①………………………………… 2分
. ①………………………………… 2分
(i) 當x≥1時,|x+1|-|(x-1)|=2.…………………………………… 5分
∴①式恒成立.
(ii) 當-1<x<1時,|x+1|-|x-1|=2x,
①式化為 即
即 ………………………………… 8分
………………………………… 8分
(iii)當x≤-1時,|x+1|-|x-1|=-2,
①式無解.
綜上, x取值范圍是 .……………………………… 10分
.……………………………… 10分
18. (本小題滿分12分)
.解:(1) ,
, ,且
,且 .
.
 ,即
,即 ,又
,又 ,
, ……..2分
……..2分
又由 ,
, 5分
5分
(2)由正弦定理得: ,
7分
,
7分
又 ,
,
 …………9分
…………9分
 ,則
,則 .則
.則 ,
,
即 的取值范圍是
的取值范圍是 …………………
12分
…………………
12分
19.(本小題滿分12分)
(1)解:設“射手射擊1次,擊中目標”為事件A
則在3次射擊中至少有兩次連續擊中目標的概率

 =
= 7分
7分
(2)解:射手第3次擊中目標時,恰好射擊了4次的概率
 12分
12分
20. (本小題滿分12分)
(Ⅰ)解: ,令
,令 ,得
,得 .
2分
.
2分






0


增
極大值
減
由上圖表知:
 的單調遞增區間為
的單調遞增區間為 ,單調遞減區間為
,單調遞減區間為 .
.
 的極大值為
的極大值為 .
5分
.
5分
(Ⅱ)證明:對一切 ,都有
,都有 成立
成立
則有
由(Ⅰ)知, 的最大值為
的最大值為 ,
,
并且 成立,
8分
成立,
8分
當且僅當 時成立,
時成立,
函數 的最小值大于等于函數
的最小值大于等于函數 的最大值,
的最大值,
但等號不能同時成立.
所以,對一切 ,都有
,都有 成立. 12分
成立. 12分
21.(本小題滿分12分)
(Ⅰ)解:由已知:對于 ,總有
,總有 ①成立
①成立
∴ (n ≥ 2)②
(n ≥ 2)②
①--②得
∴
∵ 均為正數,∴
均為正數,∴ (n ≥ 2)
(n ≥ 2)
∴數列 是公差為1的等差數列
是公差為1的等差數列
又n=1時, , 解得
, 解得 =1
=1
∴ .(
.( )
……………4分
)
……………4分
(Ⅱ)(解法一)由已知  ,
,

易得 
猜想 n≥2 時, 是遞減數列.
是遞減數列.
令
∵當
∴在 內
內 為單調遞減函數.
為單調遞減函數.
由 .
.
∴n≥2 時,  是遞減數列.即
是遞減數列.即 是遞減數列.
是遞減數列.
又 , ∴數列
, ∴數列 中的最大項為
中的最大項為 . …………… 6分
. …………… 6分
(解法二) 猜測數列 中的最大項為
中的最大項為 .
.
 易直接驗證;
易直接驗證;
以下用數學歸納法證明n≥3 時, 
(1)當 時,
時,  , 所以
, 所以 時不等式成立;
時不等式成立;
(2)假設 時不等式成立,即
時不等式成立,即 ,即
,即 ,
,
當 時,
時,  ,
,
所以 ,即
,即 時不等式成立.
時不等式成立.
由(1)(2)知 對一切不小于3的正整數都成立.
對一切不小于3的正整數都成立.
…………… 8分
(Ⅲ)(解法一)當 時,可證:
時,可證:  …………… 10分
…………… 10分
 …………… 12分
…………… 12分
(解法二)  時,
時,  ……8分
……8分

…………… 12分
注:也可分段估計,轉化為等比數列求和(也可加強命題,使用數學歸納法)
22.(本小題滿分12分)
解:(I)由

故 的方程為
的方程為 點A的坐標為(1,0)
2分
點A的坐標為(1,0)
2分
設
由
整理 4分
4分
 動點M的軌跡C為以原點為中心,焦點在x軸上,
動點M的軌跡C為以原點為中心,焦點在x軸上,
長軸長為 ,短軸長為2的橢圓。
5分
,短軸長為2的橢圓。
5分
(II)如圖,由題意知 的斜率存在且不為零,
的斜率存在且不為零,
設 方程為
方程為 ①
①
將①代入 ,整理,得
,整理,得
 7分
7分
設 、
、 ,
,
則 ②
②
令
由此可得
由②知

 ,
,
即 10分
10分


解得
又
 面積之比的取值范圍是
面積之比的取值范圍是 12分
12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com