題目列表(包括答案和解析)
（本小題滿分10分）
某射擊小組有甲、乙兩名射手，甲的命中率為
，乙的命中率為
，在射擊比武活動中每人射擊兩發子彈則完成一次檢測，在一次檢測中，若兩人命中次數相等且都不少于一發，則稱該射擊小組為“先進和諧組”.
（Ⅰ）若
，求該小組在一次檢測中榮獲“先進和諧組”的概率；
（Ⅱ）計劃在2011年每月進行1次檢測，設這12次檢測中該小組獲得“先進和諧組”的次數為
，
如果
，求的取值范圍；
（本小題滿分12分）
甲、乙兩名射手各進行一次射擊，射中環數
的分布列分別為：
 | 8 | 9 | 10 |
| P | 0．3 | 0．5 | a |
 | 8 | 9 | 10 |
| P | 0．2 | 0．3 | b |
）確定a、b的值，并求兩人各進行一次射擊，都射中10環的概率；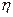
的分布列及期望，并求結束時射擊輪次超過2次的概率。
的分布列分別為： | 8 | 9 | 10 |
| P | 0．3 | 0．5 | a |
 | 8 | 9 | 10 |
| P | 0．2 | 0．3 | b |
）確定a、b的值，并求兩人各進行一次射擊，都射中10環的概率；
的分布列及期望，并求結束時射擊輪次超過2次的概率。（08年安徽信息交流文）（本小題滿分12分）某種項目的射擊比賽規定：開始時在距離目標100m處射擊，如果命中記3分，同時停止射擊；若第一次射擊未命中目標，可以進行第二次射擊，但目標已在150m遠處，這時命中記2分，同時停止射擊；若第二次射擊仍未命中，可以進行第三次射擊，但目標已在200m遠處，這時命中記1分，同時停止射擊。已知M射手在100m處命中目標的概率為
，若他命中目標的概率與距離的平方成反比，且各次射擊都是獨立的。
（1）求M射手在150m處命中目標的概率；
（2）求M射手得1分的概率；
（3）求M射手在三次射擊中命中目標的概率．（本小題滿分12分）
甲、乙兩名射手各進行一次射擊，射中環數
的分布列分別為：
|
|
8 |
9 |
10 |
|
P |
0．3 |
0．5 |
a |
|
|
8 |
9 |
10 |
|
P |
0．2 |
0．3 |
b |
（I）確定a、b的值，并求兩人各進行一次射擊，都射中10環的概率；
（II）兩各射手各射擊一次為一輪射擊，如果在某一輪射擊中兩人都射中10環，則射擊結束，否則繼續射擊，但最多不超過4輪，求結束時射擊輪次數
的分布列及期望，并求結束時射擊輪次超過2次的概率。
一、選擇題：本大題共12小題，每小題5分，共60分.
BCBBA BCDCB DA
二．填空題：本大題共4小題，每小題5分，共20分.
13. 2
14 . 
15.
4 16. 
三、解答題(本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟)
17. （本大題共10分）
解：
4分
或
8分
故原不等式的解集為
10分
18. （本小題滿分12分）
解：（1）
，
，且
.
，即
，又
，
……..2分
又由
，
5分
（2）由正弦定理得：
，
7分
又
，
…………9分
，則
.則
，
即
的取值范圍是
…………………
12分
19.（本小題滿分12分）
（1）解：設“射手射擊1次，擊中目標”為事件A
則在3次射擊中至少有兩次連續擊中目標的概率
=
7分
（2）解：射手第3次擊中目標時，恰好射擊了4次的概率
12分
20. (本小題滿分12分)
（Ⅰ）∵
∴
2分
∵
4分
∴
6分
（Ⅱ）∵函數
在區間
上單調遞增
∴
對一切
恒成立
方法1 
時成立
當
時，等價于不等式
恒成立
令
當
時取到等號，所以
∴
12分
方法2 設
對稱軸
當
時，要滿足條件，只要
成立
當
時，
，∴
當
時，只要
矛盾
綜合得
12分
21．（本小題滿分12分）
解：（Ⅰ）設
的公差為d，{Bn}的公比為q，則依題意有q>0且
解得d=2，q=2.
所以， 
，
6分
（Ⅱ）
錯位相減法得：
n=1,2,3…
12分
22．（本小題滿分12分）
解：（I）由
故
的方程為
點A的坐標為（1，0）
2分
設
由
整理
4分
M的軌跡C為以原點為中心，焦點在x軸上，長軸長為
，短軸長為2的橢圓 5分
（II）如圖，由題意知
的斜率存在且不為零，
設方程為
①
將①代入，整理，得
7分
設
、
，則
②
令
由此可得
由②知
，
即
10分
解得
又
面積之比的取值范圍是
12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
