
題目列表(包括答案和解析)
在計(jì)算“![]() ”時(shí),某同學(xué)學(xué)到了如下一種方法:
”時(shí),某同學(xué)學(xué)到了如下一種方法:
先改寫(xiě)第k項(xiàng):![]() 由此得
由此得
![]()
![]()
…
![]()
相加,得![]()
類(lèi)比上述方法,請(qǐng)你計(jì)算“![]() ”,其結(jié)果為
”,其結(jié)果為
在計(jì)算“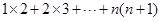 ”時(shí),某同學(xué)學(xué)到了如下一種方法:先改寫(xiě)第k項(xiàng):
”時(shí),某同學(xué)學(xué)到了如下一種方法:先改寫(xiě)第k項(xiàng):
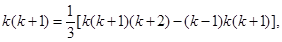 由此得
由此得
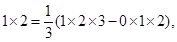
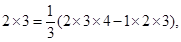
………… 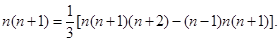
相加,得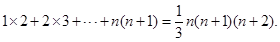
類(lèi)比上述方法,請(qǐng)你計(jì)算“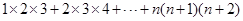 ”,
”,
其結(jié)果為
在計(jì)算 時(shí),某同學(xué)學(xué)到了如下一種方法:
時(shí),某同學(xué)學(xué)到了如下一種方法:
先改寫(xiě)第K項(xiàng):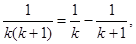
由此得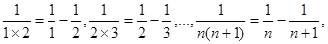
相加,得
類(lèi)比上述方法,請(qǐng)計(jì)算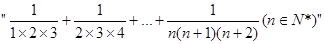 ,其結(jié)果為_(kāi)__________.
,其結(jié)果為_(kāi)__________.
在計(jì)算“ ”時(shí),某同學(xué)學(xué)到了如下一種方法:先改寫(xiě)第
”時(shí),某同學(xué)學(xué)到了如下一種方法:先改寫(xiě)第 項(xiàng):
項(xiàng): ,由此得
,由此得



相加,得
類(lèi)比上述方法,請(qǐng)你計(jì)算“ ”,其結(jié)果為
________.
”,其結(jié)果為
________.
在計(jì)算“
 ”時(shí),某同學(xué)學(xué)到了如下一種方法:
”時(shí),某同學(xué)學(xué)到了如下一種方法:
先改寫(xiě)第 項(xiàng):
項(xiàng): ,
,
由此得  ,
, ,¼,
,¼, ,
,
相加,得
類(lèi)比上述方法,請(qǐng)你計(jì)算“
 ”,
”,
其結(jié)果為 ________
1.D 2.B 3.C 4.B 5.A 6.B 7.B 8.D 9.C 10.C
l1.A 12.C
13.考理科數(shù)學(xué)試題.files/image306.gif)
14.15
15.考理科數(shù)學(xué)試題.files/image308.gif)
16.考理科數(shù)學(xué)試題.files/image310.gif)
提示:
1.D 考理科數(shù)學(xué)試題.files/image312.gif) .
.
2.B 視力住0.9以上的頻率為考理科數(shù)學(xué)試題.files/image314.gif) ,人數(shù)為
,人數(shù)為考理科數(shù)學(xué)試題.files/image316.gif) .
.
3.C 考理科數(shù)學(xué)試題.files/image318.gif) ,且
,且考理科數(shù)學(xué)試題.files/image320.gif)
若考理科數(shù)學(xué)試題.files/image056.gif) ,則
,則考理科數(shù)學(xué)試題.files/image323.gif) 且
且考理科數(shù)學(xué)試題.files/image325.gif)
反之,若考理科數(shù)學(xué)試題.files/image062.gif) ,則
,則考理科數(shù)學(xué)試題.files/image056.gif)
4.B 考理科數(shù)學(xué)試題.files/image329.gif) ,由
,由考理科數(shù)學(xué)試題.files/image331.gif) ,得
,得考理科數(shù)學(xué)試題.files/image333.gif) .
.
考理科數(shù)學(xué)試題.files/image335.gif) .
.
5.A 考理科數(shù)學(xué)試題.files/image337.gif) .
.
6.B 考理科數(shù)學(xué)試題.files/image339.gif)
當(dāng)考理科數(shù)學(xué)試題.files/image088.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image342.gif) ,由
,由考理科數(shù)學(xué)試題.files/image344.gif) 得
得考理科數(shù)學(xué)試題.files/image346.gif) ;
;
當(dāng)考理科數(shù)學(xué)試題.files/image348.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image350.gif) ;
;
當(dāng)考理科數(shù)學(xué)試題.files/image352.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image354.gif) ,由
,由考理科數(shù)學(xué)試題.files/image356.gif) .
.
7.B 該幾何體是上面是正四棱錐,下面為正方體,體積為
考理科數(shù)學(xué)試題.files/image358.gif) .
.
8.D 考理科數(shù)學(xué)試題.files/image360.gif) .
.
9.C 考理科數(shù)學(xué)試題.files/image362.gif) ,
,
考理科數(shù)學(xué)試題.files/image364.gif) ,
,
考理科數(shù)學(xué)試題.files/image366.gif) ,
,
考理科數(shù)學(xué)試題.files/image368.gif) ,
,
考理科數(shù)學(xué)試題.files/image370.gif) .
.
10.C 考理科數(shù)學(xué)試題.files/image372.gif)
即考理科數(shù)學(xué)試題.files/image348.gif) ,或
,或考理科數(shù)學(xué)試題.files/image375.gif) .
.
考理科數(shù)學(xué)試題.files/image377.gif) 設(shè)
設(shè)考理科數(shù)學(xué)試題.files/image379.gif) .
.
則考理科數(shù)學(xué)試題.files/image148.gif) 方程為
方程為考理科數(shù)學(xué)試題.files/image382.gif) .
.
考理科數(shù)學(xué)試題.files/image384.gif) 過(guò)點(diǎn)
過(guò)點(diǎn)考理科數(shù)學(xué)試題.files/image386.gif)
考理科數(shù)學(xué)試題.files/image387.jpg)
考理科數(shù)學(xué)試題.files/image389.gif) ,
,
考理科數(shù)學(xué)試題.files/image391.gif) ,
,
考理科數(shù)學(xué)試題.files/image393.gif) ,
,
考理科數(shù)學(xué)試題.files/image395.gif) .
.
12.C
畫(huà)出平面區(qū)域考理科數(shù)學(xué)試題.files/image397.gif) ,
,
圓考理科數(shù)學(xué)試題.files/image399.gif) 的圓心
的圓心考理科數(shù)學(xué)試題.files/image401.gif) ,半徑為l,
,半徑為l,
考理科數(shù)學(xué)試題.files/image403.gif) 的最大值為
的最大值為考理科數(shù)學(xué)試題.files/image405.gif) 的最小值為
的最小值為
考理科數(shù)學(xué)試題.files/image407.gif) .
.考理科數(shù)學(xué)試題.files/image409.gif) 的最大值為
的最大值為考理科數(shù)學(xué)試題.files/image411.gif) ,最小值為
,最小值為考理科數(shù)學(xué)試題.files/image413.gif)
13.考理科數(shù)學(xué)試題.files/image415.gif) .
.
考理科數(shù)學(xué)試題.files/image417.gif) ,
, 考理科數(shù)學(xué)試題.files/image419.gif) .
.
14.15 考理科數(shù)學(xué)試題.files/image421.gif) ;
;
考理科數(shù)學(xué)試題.files/image423.gif) ;
;
考理科數(shù)學(xué)試題.files/image425.gif) .
.
15.考理科數(shù)學(xué)試題.files/image427.gif)
考理科數(shù)學(xué)試題.files/image429.gif)
考理科數(shù)學(xué)試題.files/image431.gif)
考理科數(shù)學(xué)試題.files/image433.gif)
考理科數(shù)學(xué)試題.files/image435.gif)
考理科數(shù)學(xué)試題.files/image437.gif)
考理科數(shù)學(xué)試題.files/image439.gif)
考理科數(shù)學(xué)試題.files/image441.gif) .
.
16.考理科數(shù)學(xué)試題.files/image443.gif) .
.
又考理科數(shù)學(xué)試題.files/image445.gif)
考理科數(shù)學(xué)試題.files/image447.gif)
考理科數(shù)學(xué)試題.files/image449.gif)
17.解:(1)考理科數(shù)學(xué)試題.files/image451.gif) , (2分)
, (2分)
考理科數(shù)學(xué)試題.files/image453.gif) . (4分)
. (4分)
由余弦定理,得考理科數(shù)學(xué)試題.files/image455.gif) . (6分)
. (6分)
(2)考理科數(shù)學(xué)試題.files/image457.gif) , (7分)
, (7分)
考理科數(shù)學(xué)試題.files/image459.gif) (9分)
(9分) 考理科數(shù)學(xué)試題.files/image461.gif) (10分)
(10分)
考理科數(shù)學(xué)試題.files/image463.gif) (11分)
(11分)
考理科數(shù)學(xué)試題.files/image465.gif) (12分)
(12分)
18.解:(1)考理科數(shù)學(xué)試題.files/image227.gif) 的可能取值為l,2,3,4.
的可能取值為l,2,3,4.
考理科數(shù)學(xué)試題.files/image468.gif)
考理科數(shù)學(xué)試題.files/image470.gif) (4分)
(4分)
∴甲取球次數(shù)考理科數(shù)學(xué)試題.files/image227.gif) 的數(shù)學(xué)期望
的數(shù)學(xué)期望考理科數(shù)學(xué)試題.files/image473.gif) . (6分)
. (6分)
(2)由題意,兩人各自從自己的箱子里任取一球比顏色
共有考理科數(shù)學(xué)試題.files/image475.gif) (種)不同情形,
(8分)
(種)不同情形,
(8分)
每種情形都是等可能,記甲獲勝為事件A,則
考理科數(shù)學(xué)試題.files/image477.gif) (11分)
(11分)
所以甲獲勝的概率小于乙獲勝的概率,這個(gè)游戲規(guī)則不公平 (12分)
考理科數(shù)學(xué)試題.files/image479.jpg) 19.解:以
19.解:以考理科數(shù)學(xué)試題.files/image481.gif) 為原點(diǎn),
為原點(diǎn),考理科數(shù)學(xué)試題.files/image483.gif) 、
、考理科數(shù)學(xué)試題.files/image485.gif) 、
、考理科數(shù)學(xué)試題.files/image234.gif) 所在的直線(xiàn)為
所在的直線(xiàn)為
考理科數(shù)學(xué)試題.files/image488.gif) ,
,考理科數(shù)學(xué)試題.files/image490.gif) ,
,考理科數(shù)學(xué)試題.files/image492.gif) 軸,建立如圖所示的空間直角坐標(biāo)系,
軸,建立如圖所示的空間直角坐標(biāo)系,
則考理科數(shù)學(xué)試題.files/image494.gif)
考理科數(shù)學(xué)試題.files/image496.gif)
考理科數(shù)學(xué)試題.files/image498.gif)
考理科數(shù)學(xué)試題.files/image500.gif) (3分)
(3分)
(1)考理科數(shù)學(xué)試題.files/image502.gif) ,
,
考理科數(shù)學(xué)試題.files/image504.gif)
即直線(xiàn)考理科數(shù)學(xué)試題.files/image241.gif) 與
與考理科數(shù)學(xué)試題.files/image234.gif) 所成角的余角的余弦值為
所成角的余角的余弦值為考理科數(shù)學(xué)試題.files/image508.gif) (6分)
(6分)
(2)設(shè)考理科數(shù)學(xué)試題.files/image510.gif)
由考理科數(shù)學(xué)試題.files/image512.gif) 平面
平面考理科數(shù)學(xué)試題.files/image250.gif) 得
得考理科數(shù)學(xué)試題.files/image515.gif)
即考理科數(shù)學(xué)試題.files/image517.gif) 得
得考理科數(shù)學(xué)試題.files/image519.gif)
考理科數(shù)學(xué)試題.files/image521.gif) ,即
,即考理科數(shù)學(xué)試題.files/image246.gif) 為
為考理科數(shù)學(xué)試題.files/image483.gif) 的中點(diǎn). (9分)
的中點(diǎn). (9分)
(3)由(2)知考理科數(shù)學(xué)試題.files/image525.gif) 為平面
為平面考理科數(shù)學(xué)試題.files/image250.gif) 的法向量.
的法向量.
設(shè)考理科數(shù)學(xué)試題.files/image528.gif) 為平面
為平面考理科數(shù)學(xué)試題.files/image530.gif) 的法向量,
的法向量,
考理科數(shù)學(xué)試題.files/image532.gif)
由考理科數(shù)學(xué)試題.files/image534.gif) 即
即考理科數(shù)學(xué)試題.files/image536.gif)
令考理科數(shù)學(xué)試題.files/image538.gif) 得
得考理科數(shù)學(xué)試題.files/image540.gif) ,
,
考理科數(shù)學(xué)試題.files/image542.gif) ,
,
即二面角考理科數(shù)學(xué)試題.files/image252.gif) 的余弦值為
的余弦值為考理科數(shù)學(xué)試題.files/image508.gif)
考理科數(shù)學(xué)試題.files/image546.gif) (12分)
(12分)
(非向量解法參照給分)
20.(1)解:考理科數(shù)學(xué)試題.files/image548.gif) 成等比數(shù)列,
成等比數(shù)列,考理科數(shù)學(xué)試題.files/image550.gif) ,即
,即考理科數(shù)學(xué)試題.files/image552.gif)
又考理科數(shù)學(xué)試題.files/image554.gif) , (3分)
, (3分)
考理科數(shù)學(xué)試題.files/image556.gif) (5分)
(5分)
(2)證明: 考理科數(shù)學(xué)試題.files/image558.gif) . (6分)
. (6分)
考理科數(shù)學(xué)試題.files/image560.gif) 是首項(xiàng)為2,公差為2的等差數(shù)列,
是首項(xiàng)為2,公差為2的等差數(shù)列,
考理科數(shù)學(xué)試題.files/image562.gif) (7分)
(7分)
考理科數(shù)學(xué)試題.files/image564.gif)
考理科數(shù)學(xué)試題.files/image566.gif) (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)考理科數(shù)學(xué)試題.files/image568.gif) 時(shí)取“=”). ① (9分)
時(shí)取“=”). ① (9分)
考理科數(shù)學(xué)試題.files/image570.gif)
當(dāng)且僅當(dāng)考理科數(shù)學(xué)試題.files/image572.gif) 即
即考理科數(shù)學(xué)試題.files/image574.gif) 時(shí)取“=”. ② (11分)
時(shí)取“=”. ② (11分)
又①②中等號(hào)不可能同時(shí)取到,考理科數(shù)學(xué)試題.files/image576.gif) (12分)
(12分)
21.解:(1)設(shè)考理科數(shù)學(xué)試題.files/image578.gif) .
.
對(duì)稱(chēng)軸方程考理科數(shù)學(xué)試題.files/image580.gif) .由題意
.由題意考理科數(shù)學(xué)試題.files/image582.gif) 恒成立, (2分)
恒成立, (2分)
考理科數(shù)學(xué)試題.files/image584.gif) 在區(qū)間
在區(qū)間考理科數(shù)學(xué)試題.files/image586.gif) 上單凋遞增, (3分)
上單凋遞增, (3分)
∴當(dāng)且僅當(dāng)橢圓考理科數(shù)學(xué)試題.files/image151.gif) 上的點(diǎn)
上的點(diǎn)考理科數(shù)學(xué)試題.files/image115.gif) 在橢圓的左、右頂點(diǎn)時(shí)
在橢圓的左、右頂點(diǎn)時(shí)考理科數(shù)學(xué)試題.files/image283.gif) 取得最小值與最大值.(4分)
取得最小值與最大值.(4分)
(安徽高中數(shù)學(xué)網(wǎng)站注:這里用橢圓第二定義根簡(jiǎn)單直觀(guān))
(2)由已知與(1)得:考理科數(shù)學(xué)試題.files/image591.gif) ,
,
考理科數(shù)學(xué)試題.files/image593.gif) , (5分)
, (5分)
∴橢圓的標(biāo)準(zhǔn)方程為考理科數(shù)學(xué)試題.files/image595.gif) . (6分)
. (6分)
(3)設(shè)考理科數(shù)學(xué)試題.files/image597.gif) ,聯(lián)立
,聯(lián)立考理科數(shù)學(xué)試題.files/image599.gif)
得考理科數(shù)學(xué)試題.files/image601.gif) . (7分)
. (7分)
則考理科數(shù)學(xué)試題.files/image603.gif)
又考理科數(shù)學(xué)試題.files/image605.gif) ,(8分)
,(8分)
∵橢圓的右頂點(diǎn)為考理科數(shù)學(xué)試題.files/image607.gif) ,
,
考理科數(shù)學(xué)試題.files/image609.gif)
考理科數(shù)學(xué)試題.files/image611.gif)
考理科數(shù)學(xué)試題.files/image613.gif)
考理科數(shù)學(xué)試題.files/image615.gif) (9分)
(9分)
解得:考理科數(shù)學(xué)試題.files/image617.gif) ,且均滿(mǎn)足
,且均滿(mǎn)足考理科數(shù)學(xué)試題.files/image619.gif) , (10分)
, (10分)
當(dāng)考理科數(shù)學(xué)試題.files/image621.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image148.gif) 的方程為
的方程為考理科數(shù)學(xué)試題.files/image624.gif) ,直線(xiàn)過(guò)定點(diǎn)(2,0),與已知矛盾.
,直線(xiàn)過(guò)定點(diǎn)(2,0),與已知矛盾.
當(dāng)考理科數(shù)學(xué)試題.files/image626.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image148.gif) 的方程為
的方程為考理科數(shù)學(xué)試題.files/image628.gif) ,直線(xiàn)過(guò)定點(diǎn)(
,直線(xiàn)過(guò)定點(diǎn)(考理科數(shù)學(xué)試題.files/image630.gif) ,0), (11分)
,0), (11分)
∴直線(xiàn)考理科數(shù)學(xué)試題.files/image148.gif) 過(guò)定點(diǎn),定點(diǎn)坐標(biāo)為(
過(guò)定點(diǎn),定點(diǎn)坐標(biāo)為(考理科數(shù)學(xué)試題.files/image630.gif) ,0). (12分)
,0). (12分)
22,解:(1)由題意:考理科數(shù)學(xué)試題.files/image085.gif) 的定義域?yàn)?sub>
的定義域?yàn)?sub>考理科數(shù)學(xué)試題.files/image633.gif) ,且
,且考理科數(shù)學(xué)試題.files/image635.gif) .
.
考理科數(shù)學(xué)試題.files/image637.gif) ,故
,故考理科數(shù)學(xué)試題.files/image085.gif) 在
在考理科數(shù)學(xué)試題.files/image633.gif) 上是單調(diào)遞增函數(shù). (2分)
上是單調(diào)遞增函數(shù). (2分)
(2)由(1)可知:考理科數(shù)學(xué)試題.files/image639.gif)
① 若考理科數(shù)學(xué)試題.files/image641.gif) ,則
,則考理科數(shù)學(xué)試題.files/image643.gif) ,即
,即考理科數(shù)學(xué)試題.files/image645.gif) 在
在考理科數(shù)學(xué)試題.files/image297.gif) 上恒成立,此時(shí)
上恒成立,此時(shí)考理科數(shù)學(xué)試題.files/image085.gif) 在
在考理科數(shù)學(xué)試題.files/image297.gif) 上為增函數(shù),
上為增函數(shù),
考理科數(shù)學(xué)試題.files/image648.gif) (舍去). (4分)
(舍去). (4分)
② 若考理科數(shù)學(xué)試題.files/image650.gif) ,則
,則考理科數(shù)學(xué)試題.files/image652.gif) ,即
,即考理科數(shù)學(xué)試題.files/image654.gif) 在
在考理科數(shù)學(xué)試題.files/image297.gif) 上恒成立,此時(shí)
上恒成立,此時(shí)考理科數(shù)學(xué)試題.files/image085.gif) 在
在考理科數(shù)學(xué)試題.files/image297.gif) 上為減函數(shù),
上為減函數(shù),
考理科數(shù)學(xué)試題.files/image657.gif) (舍去). (6分)
(舍去). (6分)
③ 若考理科數(shù)學(xué)試題.files/image659.gif) ,令
,令考理科數(shù)學(xué)試題.files/image661.gif) 得
得考理科數(shù)學(xué)試題.files/image663.gif) ,
,
當(dāng)考理科數(shù)學(xué)試題.files/image665.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image667.gif) 在
在考理科數(shù)學(xué)試題.files/image669.gif) 上為減函數(shù),
上為減函數(shù),
當(dāng)考理科數(shù)學(xué)試題.files/image671.gif) 時(shí),
時(shí),考理科數(shù)學(xué)試題.files/image673.gif) 在
在考理科數(shù)學(xué)試題.files/image675.gif) 上為增函數(shù),
上為增函數(shù),
考理科數(shù)學(xué)試題.files/image677.gif) (9分)
(9分)
綜上可知:考理科數(shù)學(xué)試題.files/image679.gif) . (10分)(3)
. (10分)(3)考理科數(shù)學(xué)試題.files/image681.gif) .
.
又考理科數(shù)學(xué)試題.files/image683.gif) (11分)
(11分)
令考理科數(shù)學(xué)試題.files/image685.gif) ,
,
考理科數(shù)學(xué)試題.files/image687.gif) 在
在考理科數(shù)學(xué)試題.files/image689.gif) 上是減函數(shù),
上是減函數(shù),考理科數(shù)學(xué)試題.files/image691.gif) ,即
,即考理科數(shù)學(xué)試題.files/image693.gif) ,
,
考理科數(shù)學(xué)試題.files/image695.gif) 在
在考理科數(shù)學(xué)試題.files/image689.gif) 上也是減函數(shù),
上也是減函數(shù),考理科數(shù)學(xué)試題.files/image697.gif) .
.
令考理科數(shù)學(xué)試題.files/image641.gif) 得
得考理科數(shù)學(xué)試題.files/image700.gif) ,∴當(dāng)
,∴當(dāng)考理科數(shù)學(xué)試題.files/image302.gif) 在
在考理科數(shù)學(xué)試題.files/image304.gif) 恒成立時(shí),
恒成立時(shí),考理科數(shù)學(xué)試題.files/image641.gif) .(14分)
.(14分)
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com