
題目列表(包括答案和解析)
(1)求![]() ·
·![]() 的值;
的值;
(2)求點Q的縱坐標(biāo);
(3)證明|![]() |2=|
|2=|![]() |·|
|·|![]() |.
|.
(1)求![]() ·
·![]() 的值;
的值;
(2)求點Q的縱坐標(biāo);
(3)證明|![]() |2=|
|2=|![]() |·|
|·|![]() |.
|.
已知拋物線x2=2py(p>0)與雙曲線 -
-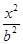 =1(a>0, b>0)有相同的焦點F,點B是兩曲線的一
=1(a>0, b>0)有相同的焦點F,點B是兩曲線的一
個交點,且BF⊥y軸,若L為雙曲線的一條漸近線,則L的傾斜角所在的區(qū)間可能是 ( )
A.(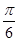 ,
,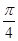 ) B.(
) B.(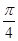 ,
,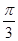 ) C.(
) C.( ,
,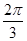 ) D.(
) D.(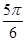 ,π)
,π)
已知拋物線x2=2py(p>0)與雙曲線 -
- =1(a>0, b>0)有相同的焦點F,點B
=1(a>0, b>0)有相同的焦點F,點B
是兩曲線的一個交點,且BF⊥y軸,若L為雙曲線的一條漸近線,則L的傾斜角所在的區(qū)間
可能是
A.(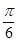 ,
,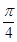 ) B.(
) B.(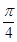 ,
, ) C.(
) C.( ,π) D.(
,π) D.( ,
, )
)
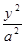 -
-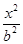 =1(a>0, b>0)有相同的焦點F,點B是兩曲線的一個交點,且BF⊥y軸,若L為雙曲線的一條漸近線,則L的傾斜角所在的區(qū)間可能是 ( )
=1(a>0, b>0)有相同的焦點F,點B是兩曲線的一個交點,且BF⊥y軸,若L為雙曲線的一條漸近線,則L的傾斜角所在的區(qū)間可能是 ( )A.(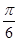 , ,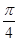 ) ) | B.(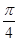 , ,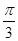 ) ) | C.(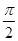 , ,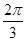 ) ) | D.(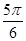 ,π) ,π) |
一、選擇題:B B AD C/ BDBCB
二、填空題:
11、10 12、3 13、21年高三第七次月考數(shù)學(xué)文科試題.files/image153.gif) 14、4 15、
14、4 15、年高三第七次月考數(shù)學(xué)文科試題.files/image155.gif)
三、解答題:
16、【解析】(1)年高三第七次月考數(shù)學(xué)文科試題.files/image157.gif) ……………………3分
……………………3分
年高三第七次月考數(shù)學(xué)文科試題.files/image159.gif) 的最小正周期
的最小正周期年高三第七次月考數(shù)學(xué)文科試題.files/image161.gif) ;……………………6分
;……………………6分
(2) 將函數(shù)f(x)沿向量年高三第七次月考數(shù)學(xué)文科試題.files/image131.gif) 得到函數(shù)g(x)=
得到函數(shù)g(x)=年高三第七次月考數(shù)學(xué)文科試題.files/image163.gif) ……9分
……9分
當(dāng)年高三第七次月考數(shù)學(xué)文科試題.files/image165.gif) 即
即年高三第七次月考數(shù)學(xué)文科試題.files/image167.gif) 時,函數(shù)g(x)單調(diào)遞減,
時,函數(shù)g(x)單調(diào)遞減,
故所求區(qū)間為年高三第七次月考數(shù)學(xué)文科試題.files/image169.gif) .………………………………………12分
.………………………………………12分
17、解:∵年高三第七次月考數(shù)學(xué)文科試題.files/image171.gif) ∴
∴年高三第七次月考數(shù)學(xué)文科試題.files/image173.gif)
年高三第七次月考數(shù)學(xué)文科試題.files/image175.gif) ①…………5分
①…………5分
又∵年高三第七次月考數(shù)學(xué)文科試題.files/image177.gif)
∴年高三第七次月考數(shù)學(xué)文科試題.files/image179.gif) ②……10分
②……10分
由①②知年高三第七次月考數(shù)學(xué)文科試題.files/image181.gif) ,即a的取值集合M=[2,3].……………………12分
,即a的取值集合M=[2,3].……………………12分
18、【解析】(1)證明:由已知AE⊥面CDO,年高三第七次月考數(shù)學(xué)文科試題.files/image183.gif) ,所以CD⊥AE
,所以CD⊥AE
又CD⊥AD,AD∩AE =A
故CD⊥平面ADE,年高三第七次月考數(shù)學(xué)文科試題.files/image185.gif)
故平面ABCD⊥平面ADE;…………………………………………4分
(2)由(1)知CD⊥AD,CD⊥ED,
故∠ADE為二面角A-CD-E的平面角.…………………………………………6分
在Rt△ADE中,sin∠ADE=年高三第七次月考數(shù)學(xué)文科試題.files/image187.gif) ,∠ADE=
,∠ADE=年高三第七次月考數(shù)學(xué)文科試題.files/image189.gif)
故平面ABCD與平面CDE所成角的平面角的大小為年高三第七次月考數(shù)學(xué)文科試題.files/image189.gif) ……………………………………8分
……………………………………8分
(3)凸多面體ABCDE為四棱錐E?ABCD,VE?ABCD = 年高三第七次月考數(shù)學(xué)文科試題.files/image191.gif) .………………………………12分
.………………………………12分
19、【解析】(1)由b2<a3,得ab<a + 2b.………………………………1分
∵1<a<b,∴ab<3b,則1<a<3.………………………………3分
又a為正整數(shù),∴a = 2.………………………………4分
∵am + 1 = bn,∴2 + (m ? 1)b + 1 = b?2n ? 1.
∴b =年高三第七次月考數(shù)學(xué)文科試題.files/image193.gif) .………………………………6分
.………………………………6分
∵b∈N*,2 n ? 1 ? m + 1 = 1.
故b = 3.………………………………8分
(2)∵an = 2 + (n ? 1)?3 = 3n ? 1,b2n + 1 = 3?22n,………………………………10分
∴cn =年高三第七次月考數(shù)學(xué)文科試題.files/image195.gif) =
=年高三第七次月考數(shù)學(xué)文科試題.files/image197.gif) .
.
∴當(dāng)n = 2或n = 3時,cn取得最小值,最小值為?12.………………………………13分
20、【解析】(1)依題意,f ′(1) = -1 + 2b + c = 0,f ′(m) = -m2 + 2bm + c = 1.………………………1分
∵-1<b<c,∴-4<-1+ 2b + c<
將c = 1 ? 2b代入-1<b<c,得?1<b<年高三第七次月考數(shù)學(xué)文科試題.files/image149.gif) .………………………………3分
.………………………………3分
將c = 1? 2b代入-m2 + 2bm + c = 1,得 -m2 + 2bm ? 2b = 0.
由年高三第七次月考數(shù)學(xué)文科試題.files/image200.gif) = 4b2 - 8b≥0,得b≤0或b≥2.………………………………5分
= 4b2 - 8b≥0,得b≤0或b≥2.………………………………5分
綜上所述,-1<年高三第七次月考數(shù)學(xué)文科試題.files/image145.gif) ≤0.………………………………6分
≤0.………………………………6分
(2)由f′(x)<1,得 -x2 + 2bx ? 2b<0.
∴x2 年高三第七次月考數(shù)學(xué)文科試題.files/image202.gif) ,………………………………8分
,………………………………8分
易知年高三第七次月考數(shù)學(xué)文科試題.files/image204.gif) 為關(guān)于
為關(guān)于年高三第七次月考數(shù)學(xué)文科試題.files/image145.gif) 的一次函數(shù).………………………………9分
的一次函數(shù).………………………………9分
依題意,不等式g(年高三第七次月考數(shù)學(xué)文科試題.files/image145.gif) )>0對-1<
)>0對-1<年高三第七次月考數(shù)學(xué)文科試題.files/image145.gif) ≤0恒成立,
≤0恒成立,
∴年高三第七次月考數(shù)學(xué)文科試題.files/image207.gif) 得x≤
得x≤年高三第七次月考數(shù)學(xué)文科試題.files/image209.gif) 或x≥
或x≥年高三第七次月考數(shù)學(xué)文科試題.files/image211.gif) .………………………………12分
.………………………………12分
∴k≥年高三第七次月考數(shù)學(xué)文科試題.files/image211.gif) ,即k的最小值為
,即k的最小值為年高三第七次月考數(shù)學(xué)文科試題.files/image211.gif) .………………………………13分
.………………………………13分
21、【解析】(1)設(shè)△PF
|F2E| = |F2Q|.
∵|PF1| ? |PF2| =
∴Q(1,0)為雙曲線的右頂點,即a = 1.………………………………3分
又|F1Q| = a + c = 4,∴c = 3,則b2 = c2 ? a2 = 8.
故雙曲線方程為年高三第七次月考數(shù)學(xué)文科試題.files/image213.gif) .………………………………5分
.………………………………5分
(2)設(shè)R年高三第七次月考數(shù)學(xué)文科試題.files/image215.gif) (t≠0)、N(x0,y0),由R、B、N三點共線,得
(t≠0)、N(x0,y0),由R、B、N三點共線,得年高三第七次月考數(shù)學(xué)文科試題.files/image217.gif) ,即
,即年高三第七次月考數(shù)學(xué)文科試題.files/image219.gif) =
=年高三第七次月考數(shù)學(xué)文科試題.files/image221.gif) ,于是
,于是年高三第七次月考數(shù)學(xué)文科試題.files/image223.gif) 解得
解得年高三第七次月考數(shù)學(xué)文科試題.files/image225.gif) ,則R
,則R年高三第七次月考數(shù)學(xué)文科試題.files/image227.gif) .………………………………6分
.………………………………6分
∵年高三第七次月考數(shù)學(xué)文科試題.files/image229.gif) ,
,年高三第七次月考數(shù)學(xué)文科試題.files/image231.gif) ,
,
∴年高三第七次月考數(shù)學(xué)文科試題.files/image233.gif) .………………………………8分
.………………………………8分
又點N在雙曲線上,∴年高三第七次月考數(shù)學(xué)文科試題.files/image235.gif) .
.
∴年高三第七次月考數(shù)學(xué)文科試題.files/image237.gif) .………………………………9分
.………………………………9分
∵x0≥1,∴AN?AR<0,∴∠RAN為鈍角.
又∠RAN與∠MAN互補,∴∠MAN為銳角.………………………………11分
故點A在以MN為直徑的圓的外部.………………………………13分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com