
題目列表(包括答案和解析)
(09年湖北八校聯(lián)考文)(13分)過![]() 軸上動(dòng)點(diǎn)
軸上動(dòng)點(diǎn)![]() 引拋物線
引拋物線![]() 的兩條切線
的兩條切線![]() ,
,![]() ,
,![]() ,
,![]() 為切點(diǎn).
為切點(diǎn).
(Ⅰ)若切線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() 和
和![]() ,求證:
,求證:![]() 為定值,并求出定值.
為定值,并求出定值.
(Ⅱ) 求證:直線![]() 恒過定點(diǎn),并求出定點(diǎn)坐標(biāo).
恒過定點(diǎn),并求出定點(diǎn)坐標(biāo).
(Ⅲ)當(dāng)![]() 最小時(shí),求
最小時(shí),求![]() 的值.
的值.
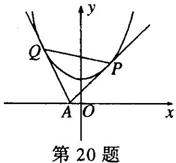
本小題滿分14分)
過 軸上動(dòng)點(diǎn)
軸上動(dòng)點(diǎn) 引拋物線
引拋物線 的兩條切線
的兩條切線 、
、 ,
, 、
、 為切點(diǎn),設(shè)切線
為切點(diǎn),設(shè)切線 、
、 的斜率分別為
的斜率分別為 和
和 .
.

(1)求證: ;
;
(2)求證:直線 恒過定點(diǎn),并求出此定點(diǎn)坐標(biāo);
恒過定點(diǎn),并求出此定點(diǎn)坐標(biāo);
(3)設(shè) 的面積為
的面積為 ,當(dāng)
,當(dāng) 最小時(shí),求
最小時(shí),求 的值.
的值.
(本小題滿分14分)
過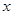 軸上動(dòng)點(diǎn)
軸上動(dòng)點(diǎn)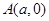 引拋物線
引拋物線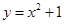 的兩條切線
的兩條切線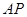 、
、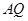 ,
,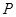 、
、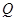 為切點(diǎn),設(shè)切線
為切點(diǎn),設(shè)切線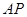 ,
,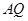 的斜率分別為
的斜率分別為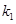 和
和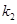 .
.
(1)求證: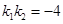 ;
;
(2) 試問:直線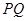 是否經(jīng)過定點(diǎn)?若是,求出該定點(diǎn)坐標(biāo);若不是,請(qǐng)說明理由.
是否經(jīng)過定點(diǎn)?若是,求出該定點(diǎn)坐標(biāo);若不是,請(qǐng)說明理由.
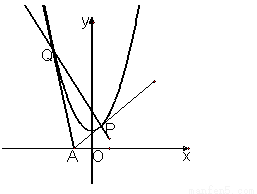
(本小題滿分12分)
過![]() 軸上動(dòng)點(diǎn)
軸上動(dòng)點(diǎn)![]() 引拋物線
引拋物線![]() 的兩條切線
的兩條切線![]() 、
、![]() ,
,![]() 、
、![]() 為切點(diǎn).
為切點(diǎn).
 (1)若切線
(1)若切線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() 和
和![]() ,求證:
,求證: ![]() 為定值,并求出定值;
為定值,并求出定值;
(2)求證:直線![]() 恒過定點(diǎn),并求出定點(diǎn)坐標(biāo);
恒過定點(diǎn),并求出定點(diǎn)坐標(biāo);
(3)當(dāng)![]() 最小時(shí),求
最小時(shí),求![]() 的值.
的值.
(本小題滿分14分)過![]() 軸上動(dòng)點(diǎn)
軸上動(dòng)點(diǎn)![]() 引拋物線
引拋物線![]() 的兩條切線
的兩條切線![]() 、
、![]() ,
,![]() 、
、![]() 為切點(diǎn),設(shè)切線
為切點(diǎn),設(shè)切線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 和
和![]() .
.
(1)求證:![]() ;
;
(2)求證:直線![]() 恒過定點(diǎn),并求出此定點(diǎn)坐標(biāo);
恒過定點(diǎn),并求出此定點(diǎn)坐標(biāo);
(3)設(shè)![]() 的面積為
的面積為![]() ,當(dāng)
,當(dāng)![]() 最小時(shí),求
最小時(shí),求![]() 的值.
的值.

一、考%20數(shù)學(xué)文科.files/image293.gif)
二、11.210 12. 考%20數(shù)學(xué)文科.files/image295.gif) 13.2 14.
13.2 14.考%20數(shù)學(xué)文科.files/image297.gif) 15.
15. 考%20數(shù)學(xué)文科.files/image299.gif) 或
或考%20數(shù)學(xué)文科.files/image091.gif) 或
或考%20數(shù)學(xué)文科.files/image302.gif)
三.解答題:
16. 解:(1)考%20數(shù)學(xué)文科.files/image304.gif)
考%20數(shù)學(xué)文科.files/image306.gif)
考%20數(shù)學(xué)文科.files/image308.gif)
考%20數(shù)學(xué)文科.files/image310.gif) ……………………………………………………………3分
……………………………………………………………3分
由題意得周期考%20數(shù)學(xué)文科.files/image312.gif) ,故
,故考%20數(shù)學(xué)文科.files/image314.gif) …………………………………………4分
…………………………………………4分
又圖象過點(diǎn)考%20數(shù)學(xué)文科.files/image316.gif) ,所以
,所以考%20數(shù)學(xué)文科.files/image318.gif)
即考%20數(shù)學(xué)文科.files/image320.gif) ,而
,而考%20數(shù)學(xué)文科.files/image322.gif) ,所以
,所以考%20數(shù)學(xué)文科.files/image324.gif)
∴考%20數(shù)學(xué)文科.files/image326.gif) ……………………………………………………6分
……………………………………………………6分
(2)當(dāng)考%20數(shù)學(xué)文科.files/image328.gif) 時(shí),
時(shí),考%20數(shù)學(xué)文科.files/image330.gif)
∴當(dāng)考%20數(shù)學(xué)文科.files/image332.gif) 時(shí),即
時(shí),即考%20數(shù)學(xué)文科.files/image334.gif) 時(shí),
時(shí),考%20數(shù)學(xué)文科.files/image195.gif) 是減函數(shù)
是減函數(shù)
當(dāng)考%20數(shù)學(xué)文科.files/image337.gif) 時(shí),即
時(shí),即考%20數(shù)學(xué)文科.files/image339.gif) 時(shí),
時(shí),考%20數(shù)學(xué)文科.files/image195.gif) 是增函數(shù)
是增函數(shù)
∴函數(shù)考%20數(shù)學(xué)文科.files/image195.gif) 的單調(diào)減區(qū)間是
的單調(diào)減區(qū)間是考%20數(shù)學(xué)文科.files/image343.gif) ,單調(diào)增區(qū)間是
,單調(diào)增區(qū)間是考%20數(shù)學(xué)文科.files/image345.gif) ………………12分
………………12分
考%20數(shù)學(xué)文科.files/image174.jpg) 17.解:
17.解:考%20數(shù)學(xué)文科.files/image174.jpg) 記“甲回答對(duì)這道題”、“ 乙回答對(duì)這道題”、“丙回答對(duì)這道題”分別為事件
記“甲回答對(duì)這道題”、“ 乙回答對(duì)這道題”、“丙回答對(duì)這道題”分別為事件考%20數(shù)學(xué)文科.files/image032.gif) 、
、考%20數(shù)學(xué)文科.files/image034.gif) 、
、考%20數(shù)學(xué)文科.files/image036.gif) ,則
,則考%20數(shù)學(xué)文科.files/image350.gif) ,且有
,且有考%20數(shù)學(xué)文科.files/image352.gif) ,即
,即考%20數(shù)學(xué)文科.files/image354.gif)
∴考%20數(shù)學(xué)文科.files/image356.gif) ……………………………………………………………………6分
……………………………………………………………………6分
(2)由(1)考%20數(shù)學(xué)文科.files/image358.gif) ,
,考%20數(shù)學(xué)文科.files/image360.gif) .
.
則甲、乙、丙三人中恰有兩人回答對(duì)該題的概率為:
考%20數(shù)學(xué)文科.files/image362.gif) ……………………12分
……………………12分
18. 解法一 公理化法
(1)當(dāng)考%20數(shù)學(xué)文科.files/image364.gif) 時(shí),取
時(shí),取考%20數(shù)學(xué)文科.files/image170.gif) 的中點(diǎn)
的中點(diǎn)考%20數(shù)學(xué)文科.files/image367.gif) ,連接
,連接考%20數(shù)學(xué)文科.files/image369.gif) ,因?yàn)?sub>
,因?yàn)?sub>考%20數(shù)學(xué)文科.files/image139.gif) 為正三角形,則
為正三角形,則考%20數(shù)學(xué)文科.files/image372.gif) ,由于
,由于考%20數(shù)學(xué)文科.files/image211.gif) 為
為考%20數(shù)學(xué)文科.files/image375.gif) 的中點(diǎn)時(shí),
的中點(diǎn)時(shí),考%20數(shù)學(xué)文科.files/image377.gif)
考%20數(shù)學(xué)文科.files/image387.gif) ∵
∵考%20數(shù)學(xué)文科.files/image389.gif) 平面
平面考%20數(shù)學(xué)文科.files/image391.gif) ,∴
,∴考%20數(shù)學(xué)文科.files/image393.gif) 平面
平面考%20數(shù)學(xué)文科.files/image391.gif) ,∴
,∴考%20數(shù)學(xué)文科.files/image396.gif) .………………………………………………4分
.………………………………………………4分
(2)當(dāng)考%20數(shù)學(xué)文科.files/image219.gif) 時(shí),過
時(shí),過考%20數(shù)學(xué)文科.files/image211.gif) 作
作考%20數(shù)學(xué)文科.files/image400.gif) 于
于考%20數(shù)學(xué)文科.files/image402.gif) ,如圖所示,則
,如圖所示,則考%20數(shù)學(xué)文科.files/image404.gif) 底面
底面考%20數(shù)學(xué)文科.files/image095.gif) ,過
,過考%20數(shù)學(xué)文科.files/image402.gif) 作
作考%20數(shù)學(xué)文科.files/image408.gif) 于
于考%20數(shù)學(xué)文科.files/image410.gif) ,連結(jié)
,連結(jié)考%20數(shù)學(xué)文科.files/image412.gif) ,則
,則考%20數(shù)學(xué)文科.files/image414.gif) ,
,考%20數(shù)學(xué)文科.files/image416.gif) 為二面角
為二面角考%20數(shù)學(xué)文科.files/image221.gif) 的平面角,
的平面角,
又考%20數(shù)學(xué)文科.files/image419.gif) ,
,考%20數(shù)學(xué)文科.files/image421.gif)
考%20數(shù)學(xué)文科.files/image423.gif) 又
又考%20數(shù)學(xué)文科.files/image425.gif)
考%20數(shù)學(xué)文科.files/image427.gif) ,
,
考%20數(shù)學(xué)文科.files/image429.gif)
考%20數(shù)學(xué)文科.files/image431.gif) ,即二面角
,即二面角考%20數(shù)學(xué)文科.files/image221.gif) 的大小為
的大小為考%20數(shù)學(xué)文科.files/image433.gif) .…………………………………………………8分
.…………………………………………………8分
(3)設(shè)考%20數(shù)學(xué)文科.files/image223.gif) 到面
到面考%20數(shù)學(xué)文科.files/image225.gif) 的距離為
的距離為考%20數(shù)學(xué)文科.files/image437.gif) ,則
,則考%20數(shù)學(xué)文科.files/image439.gif)
考%20數(shù)學(xué)文科.files/image419.gif) ,
,考%20數(shù)學(xué)文科.files/image442.gif) 平面
平面考%20數(shù)學(xué)文科.files/image444.gif) ,
,
考%20數(shù)學(xué)文科.files/image446.gif) 即為
即為考%20數(shù)學(xué)文科.files/image211.gif) 點(diǎn)到平面
點(diǎn)到平面考%20數(shù)學(xué)文科.files/image444.gif) 的距離,
的距離,
又考%20數(shù)學(xué)文科.files/image449.gif) ,
,
考%20數(shù)學(xué)文科.files/image451.gif) 即
即考%20數(shù)學(xué)文科.files/image453.gif) 解得
解得考%20數(shù)學(xué)文科.files/image455.gif) ,
,
即考%20數(shù)學(xué)文科.files/image223.gif) 到平面
到平面考%20數(shù)學(xué)文科.files/image225.gif) 的距離為
的距離為考%20數(shù)學(xué)文科.files/image457.gif) .…………………………………………………………………………12分
.…………………………………………………………………………12分
解法二 向量法
以考%20數(shù)學(xué)文科.files/image032.gif) 為原點(diǎn),
為原點(diǎn),考%20數(shù)學(xué)文科.files/image170.gif) 為
為考%20數(shù)學(xué)文科.files/image109.gif) 軸,過
軸,過考%20數(shù)學(xué)文科.files/image032.gif) 點(diǎn)與
點(diǎn)與考%20數(shù)學(xué)文科.files/image170.gif) 垂直的直線為
垂直的直線為考%20數(shù)學(xué)文科.files/image159.gif) 軸,
軸,考%20數(shù)學(xué)文科.files/image463.gif) 為
為考%20數(shù)學(xué)文科.files/image465.gif) 軸,建立空間直角坐標(biāo)系
軸,建立空間直角坐標(biāo)系考%20數(shù)學(xué)文科.files/image467.gif) ,如圖所示,
,如圖所示,
考%20數(shù)學(xué)文科.files/image471.gif) 設(shè)
設(shè)考%20數(shù)學(xué)文科.files/image473.gif) ,則
,則考%20數(shù)學(xué)文科.files/image475.gif)
(1)由考%20數(shù)學(xué)文科.files/image364.gif) 得
得考%20數(shù)學(xué)文科.files/image477.gif) ,
,
則考%20數(shù)學(xué)文科.files/image479.gif) ,
,
考%20數(shù)學(xué)文科.files/image481.gif) ,
,考%20數(shù)學(xué)文科.files/image483.gif) ………………………………4分
………………………………4分
(2)當(dāng)考%20數(shù)學(xué)文科.files/image219.gif) 時(shí),
時(shí),考%20數(shù)學(xué)文科.files/image211.gif) 點(diǎn)的坐標(biāo)是
點(diǎn)的坐標(biāo)是考%20數(shù)學(xué)文科.files/image486.gif)
設(shè)平面考%20數(shù)學(xué)文科.files/image225.gif) 的一個(gè)法向量
的一個(gè)法向量考%20數(shù)學(xué)文科.files/image489.gif) ,則
,則考%20數(shù)學(xué)文科.files/image491.gif) 即
即考%20數(shù)學(xué)文科.files/image493.gif)
考%20數(shù)學(xué)文科.files/image495.gif) 取
取考%20數(shù)學(xué)文科.files/image497.gif) ,則
,則考%20數(shù)學(xué)文科.files/image499.gif) ,
,考%20數(shù)學(xué)文科.files/image501.gif)
又平面考%20數(shù)學(xué)文科.files/image095.gif) 的一個(gè)法向量為
的一個(gè)法向量為考%20數(shù)學(xué)文科.files/image504.gif)
考%20數(shù)學(xué)文科.files/image506.gif)
又由于二面角考%20數(shù)學(xué)文科.files/image221.gif) 是一個(gè)銳角,則二面角
是一個(gè)銳角,則二面角考%20數(shù)學(xué)文科.files/image221.gif) 的大小是
的大小是考%20數(shù)學(xué)文科.files/image433.gif) .……………………8分
.……………………8分
(3)設(shè)考%20數(shù)學(xué)文科.files/image223.gif) 到面
到面考%20數(shù)學(xué)文科.files/image225.gif) 的距離為
的距離為考%20數(shù)學(xué)文科.files/image437.gif) ,
,
則考%20數(shù)學(xué)文科.files/image508.gif)
考%20數(shù)學(xué)文科.files/image510.gif)
考%20數(shù)學(xué)文科.files/image223.gif) 到平面
到平面考%20數(shù)學(xué)文科.files/image225.gif) 的距離為
的距離為考%20數(shù)學(xué)文科.files/image457.gif) .………………………………………………………………………12分
.………………………………………………………………………12分
19. 解:(Ⅰ)由于考%20數(shù)學(xué)文科.files/image512.gif) ,
,
故在點(diǎn)考%20數(shù)學(xué)文科.files/image514.gif) 處的切線方程是
處的切線方程是考%20數(shù)學(xué)文科.files/image516.gif) …………………………………………2分
…………………………………………2分
即考%20數(shù)學(xué)文科.files/image518.gif) ,故
,故考%20數(shù)學(xué)文科.files/image232.gif) 與
與考%20數(shù)學(xué)文科.files/image518.gif) 表示同一條直線,
表示同一條直線,
考%20數(shù)學(xué)文科.files/image521.gif) ,
,考%20數(shù)學(xué)文科.files/image523.gif) 即
即考%20數(shù)學(xué)文科.files/image525.gif) ,
,考%20數(shù)學(xué)文科.files/image527.gif) ,
,考%20數(shù)學(xué)文科.files/image529.gif) .……6分
.……6分
(Ⅱ) 由于考%20數(shù)學(xué)文科.files/image531.gif) ,
,
則考%20數(shù)學(xué)文科.files/image533.gif) 或
或考%20數(shù)學(xué)文科.files/image535.gif) ,所以函數(shù)
,所以函數(shù)考%20數(shù)學(xué)文科.files/image195.gif) 的單調(diào)區(qū)間是
的單調(diào)區(qū)間是考%20數(shù)學(xué)文科.files/image538.gif) ,…………………………8分
,…………………………8分
故考%20數(shù)學(xué)文科.files/image540.gif) 或
或考%20數(shù)學(xué)文科.files/image542.gif) 或
或考%20數(shù)學(xué)文科.files/image544.gif)
考%20數(shù)學(xué)文科.files/image546.gif) 或
或考%20數(shù)學(xué)文科.files/image548.gif) 或
或考%20數(shù)學(xué)文科.files/image550.gif) ,
,考%20數(shù)學(xué)文科.files/image552.gif) 或
或考%20數(shù)學(xué)文科.files/image554.gif) 或
或考%20數(shù)學(xué)文科.files/image550.gif)
考%20數(shù)學(xué)文科.files/image510.gif) 實(shí)數(shù)
實(shí)數(shù)考%20數(shù)學(xué)文科.files/image237.gif) 的取值范圍是
的取值范圍是考%20數(shù)學(xué)文科.files/image559.gif) .………………………………………………………12分
.………………………………………………………12分
20. 解:(Ⅰ)設(shè)過考%20數(shù)學(xué)文科.files/image561.gif) 與拋物線
與拋物線考%20數(shù)學(xué)文科.files/image563.gif) 的相切的直線的斜率是
的相切的直線的斜率是考%20數(shù)學(xué)文科.files/image237.gif) ,
,
則該切線的方程為:考%20數(shù)學(xué)文科.files/image566.gif)
由考%20數(shù)學(xué)文科.files/image568.gif) 得
得考%20數(shù)學(xué)文科.files/image570.gif)
考%20數(shù)學(xué)文科.files/image572.gif) ,
,
則考%20數(shù)學(xué)文科.files/image574.gif) 都是方程
都是方程考%20數(shù)學(xué)文科.files/image576.gif) 的解,故
的解,故考%20數(shù)學(xué)文科.files/image578.gif) ………………………………………………4分
………………………………………………4分
(Ⅱ)設(shè)考%20數(shù)學(xué)文科.files/image580.gif)
由于考%20數(shù)學(xué)文科.files/image582.gif) ,故切線
,故切線考%20數(shù)學(xué)文科.files/image244.gif) 的方程是:
的方程是:考%20數(shù)學(xué)文科.files/image585.gif) ,又由于
,又由于考%20數(shù)學(xué)文科.files/image032.gif) 點(diǎn)在
點(diǎn)在考%20數(shù)學(xué)文科.files/image244.gif) 上,則
上,則考%20數(shù)學(xué)文科.files/image588.gif)
則考%20數(shù)學(xué)文科.files/image590.gif) ,
,
考%20數(shù)學(xué)文科.files/image592.gif) ,同理
,同理考%20數(shù)學(xué)文科.files/image594.gif)
則直線考%20數(shù)學(xué)文科.files/image259.gif) 的方程是
的方程是考%20數(shù)學(xué)文科.files/image597.gif) ,則直線
,則直線考%20數(shù)學(xué)文科.files/image259.gif) 過定點(diǎn)
過定點(diǎn)考%20數(shù)學(xué)文科.files/image599.gif) .………………………………………8分
.………………………………………8分
(Ⅲ)要使考%20數(shù)學(xué)文科.files/image261.gif) 最小,就是使得
最小,就是使得考%20數(shù)學(xué)文科.files/image032.gif) 到直線
到直線考%20數(shù)學(xué)文科.files/image259.gif) 的距離最小,
的距離最小,
而考%20數(shù)學(xué)文科.files/image032.gif) 到直線
到直線考%20數(shù)學(xué)文科.files/image259.gif) 的距離
的距離考%20數(shù)學(xué)文科.files/image603.gif) ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)考%20數(shù)學(xué)文科.files/image605.gif) 即
即考%20數(shù)學(xué)文科.files/image607.gif) 時(shí)取等號(hào).………………………………………………………………10分
時(shí)取等號(hào).………………………………………………………………10分
設(shè)考%20數(shù)學(xué)文科.files/image580.gif)
由考%20數(shù)學(xué)文科.files/image609.gif) 得
得考%20數(shù)學(xué)文科.files/image611.gif) ,則
,則考%20數(shù)學(xué)文科.files/image613.gif)
考%20數(shù)學(xué)文科.files/image615.gif)
考%20數(shù)學(xué)文科.files/image617.gif) .…………13分
.…………13分
21. 解:(Ⅰ)由題意知考%20數(shù)學(xué)文科.files/image619.gif) 即
即考%20數(shù)學(xué)文科.files/image621.gif) ……1分
……1分
考%20數(shù)學(xué)文科.files/image623.gif)
考%20數(shù)學(xué)文科.files/image625.gif)
考%20數(shù)學(xué)文科.files/image627.gif) …………3分
…………3分
檢驗(yàn)知考%20數(shù)學(xué)文科.files/image629.gif) 時(shí),結(jié)論也成立
時(shí),結(jié)論也成立
故考%20數(shù)學(xué)文科.files/image631.gif) .………………………………………………………………………………4分
.………………………………………………………………………………4分
(Ⅱ) ①由于考%20數(shù)學(xué)文科.files/image633.gif)
故考%20數(shù)學(xué)文科.files/image635.gif)
考%20數(shù)學(xué)文科.files/image637.gif)
考%20數(shù)學(xué)文科.files/image639.gif) ………………………………………………9分
………………………………………………9分
②若考%20數(shù)學(xué)文科.files/image291.gif) ,其中
,其中考%20數(shù)學(xué)文科.files/image285.gif) ,則有
,則有考%20數(shù)學(xué)文科.files/image643.gif) ,則
,則考%20數(shù)學(xué)文科.files/image645.gif) ,
,
故考%20數(shù)學(xué)文科.files/image647.gif) ,
,
取考%20數(shù)學(xué)文科.files/image649.gif) (其中
(其中考%20數(shù)學(xué)文科.files/image651.gif) 表示不超過
表示不超過考%20數(shù)學(xué)文科.files/image109.gif) 的最大整數(shù)),則當(dāng)
的最大整數(shù)),則當(dāng)考%20數(shù)學(xué)文科.files/image289.gif) 時(shí),
時(shí),考%20數(shù)學(xué)文科.files/image291.gif) . ………………………………………………………14分
. ………………………………………………………14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com