
題目列表(包括答案和解析)
若![]() ,且
,且![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
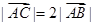 ,且
,且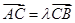 ,則
,則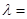
A.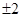 | B.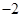 | C.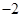 或 或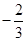 | D.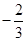 |
若![]() ,且
,且![]() ,則
,則![]()
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
![]()
[ ]
A
.{x│x∈R且x≠3} B.{x│-1≤x≤1}C
.{x│x≤1或x≥5} D.{x│1≤x≤5}若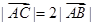 ,且
,且 ,則
,則
A. | B. | C. 或 或 | D. |
一、
二、11.210 12.  13.2 14.
13.2 14. 15.
15.  或
或 或
或
三.解答題:
16. 解:(1)


 ……………………………………………………………3分
……………………………………………………………3分
由題意得周期 ,故
,故 …………………………………………4分
…………………………………………4分
又圖象過點 ,所以
,所以
即 ,而
,而 ,所以
,所以
∴ ……………………………………………………6分
……………………………………………………6分
(2)當 時,
時,
∴當 時,即
時,即 時,
時, 是減函數
是減函數
當 時,即
時,即 時,
時, 是增函數
是增函數
∴函數 的單調減區間是
的單調減區間是 ,單調增區間是
,單調增區間是 ………………12分
………………12分
 17.解:
17.解: 記“甲回答對這道題”、“ 乙回答對這道題”、“丙回答對這道題”分別為事件
記“甲回答對這道題”、“ 乙回答對這道題”、“丙回答對這道題”分別為事件 、
、 、
、 ,則
,則 ,且有
,且有 ,即
,即
∴ ……………………………………………………………………6分
……………………………………………………………………6分
(2)由(1) ,
, .
.
則甲、乙、丙三人中恰有兩人回答對該題的概率為:
 ……………………12分
……………………12分
18. 解法一 公理化法
(1)當 時,取
時,取 的中點
的中點 ,連接
,連接 ,因為
,因為 為正三角形,則
為正三角形,則 ,由于
,由于 為
為 的中點時,
的中點時,
 ∵
∵ 平面
平面 ,∴
,∴ 平面
平面 ,∴
,∴ .………………………………………………4分
.………………………………………………4分
(2)當 時,過
時,過 作
作 于
于 ,如圖所示,則
,如圖所示,則 底面
底面 ,過
,過 作
作 于
于 ,連結
,連結 ,則
,則 ,
, 為二面角
為二面角 的平面角,
的平面角,
又 ,
,
 又
又
 ,
,

 ,即二面角
,即二面角 的大小為
的大小為 .…………………………………………………8分
.…………………………………………………8分
(3)設 到面
到面 的距離為
的距離為 ,則
,則
 ,
, 平面
平面 ,
,
 即為
即為 點到平面
點到平面 的距離,
的距離,
又 ,
,
 即
即 解得
解得 ,
,
即 到平面
到平面 的距離為
的距離為 .…………………………………………………………………………12分
.…………………………………………………………………………12分
解法二 向量法
以 為原點,
為原點, 為
為 軸,過
軸,過 點與
點與 垂直的直線為
垂直的直線為 軸,
軸, 為
為 軸,建立空間直角坐標系
軸,建立空間直角坐標系 ,如圖所示,
,如圖所示,
 設
設 ,則
,則
(1)由 得
得 ,
,
則 ,
,
 ,
, ………………………………4分
………………………………4分
(2)當 時,
時, 點的坐標是
點的坐標是
設平面 的一個法向量
的一個法向量 ,則
,則 即
即
 取
取 ,則
,則 ,
,
又平面 的一個法向量為
的一個法向量為

又由于二面角 是一個銳角,則二面角
是一個銳角,則二面角 的大小是
的大小是 .……………………8分
.……………………8分
(3)設 到面
到面 的距離為
的距離為 ,
,
則

 到平面
到平面 的距離為
的距離為 .………………………………………………………………………12分
.………………………………………………………………………12分
19. 解:(Ⅰ)由于 ,
,
故在點 處的切線方程是
處的切線方程是 …………………………………………2分
…………………………………………2分
即 ,故
,故 與
與 表示同一條直線,
表示同一條直線,
 ,
, 即
即 ,
, ,
, .……6分
.……6分
(Ⅱ) 由于 ,
,
則 或
或 ,所以函數
,所以函數 的單調區間是
的單調區間是 ,…………………………8分
,…………………………8分
故 或
或 或
或
 或
或 或
或 ,
, 或
或 或
或
 實數
實數 的取值范圍是
的取值范圍是 .………………………………………………………12分
.………………………………………………………12分
20. 解:(Ⅰ)設過 與拋物線
與拋物線 的相切的直線的斜率是
的相切的直線的斜率是 ,
,
則該切線的方程為:
由 得
得
 ,
,
則 都是方程
都是方程 的解,故
的解,故 ………………………………………………4分
………………………………………………4分
(Ⅱ)設
由于 ,故切線
,故切線 的方程是:
的方程是: ,又由于
,又由于 點在
點在 上,則
上,則
則 ,
,
 ,同理
,同理
則直線 的方程是
的方程是 ,則直線
,則直線 過定點
過定點 .………………………………………8分
.………………………………………8分
(Ⅲ)要使 最小,就是使得
最小,就是使得 到直線
到直線 的距離最小,
的距離最小,
而 到直線
到直線 的距離
的距離 ,當且僅當
,當且僅當 即
即 時取等號.………………………………………………………………10分
時取等號.………………………………………………………………10分
設
由 得
得 ,則
,則

 .…………13分
.…………13分
21. 解:(Ⅰ)由題意知 即
即 ……1分
……1分


 …………3分
…………3分
檢驗知 時,結論也成立
時,結論也成立
故 .………………………………………………………………………………4分
.………………………………………………………………………………4分
(Ⅱ) ①由于
故

 ………………………………………………9分
………………………………………………9分
②若 ,其中
,其中 ,則有
,則有 ,則
,則 ,
,
故 ,
,
取 (其中
(其中 表示不超過
表示不超過 的最大整數),則當
的最大整數),則當 時,
時, . ………………………………………………………14分
. ………………………………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com