欧美激情一级欧美精品,超碰97网站,欧美大尺度做爰床戏

12．如圖.F為橢圓的焦點(diǎn).橢圓上的點(diǎn)Mi與M7-i(i=1.2.3)關(guān)于x軸對(duì)稱.則|M1F|+|M2F|+-+|M6F|= . 【查看更多】

題目列表(包括答案和解析)

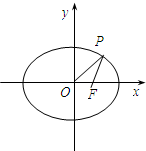
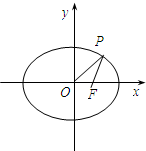如圖，F(xiàn)為橢圓

=1(a＞b＞0)的右焦點(diǎn)，P為橢圓上一點(diǎn)，O為原點(diǎn)，記△OFP的面積為S，且

•

=1．
（1）設(shè)

＜S＜

，求向量

與

夾角的取值范圍．
（2）設(shè)|

|=c，S=

c，當(dāng)c≥2時(shí)，求當(dāng)|

|取最小值時(shí)的橢圓方程．

查看答案和解析>>

如圖，F(xiàn)為橢圓

=1(a＞b＞0)的右焦點(diǎn)，P為橢圓上一點(diǎn)，O為原點(diǎn)，記△OFP的面積為S，且

•

=1．
（1）設(shè)

＜S＜

，求向量

與

夾角的取值范圍．
（2）設(shè)|

|=c，S=

c，當(dāng)c≥2時(shí)，求當(dāng)|

|取最小值時(shí)的橢圓方程．

查看答案和解析>>

如圖，F(xiàn)是橢圓的右焦點(diǎn)，以點(diǎn)F為圓心的圓過(guò)原點(diǎn)O和橢圓的右頂點(diǎn)，設(shè)P是橢圓上的動(dòng)點(diǎn)，P到橢圓兩焦點(diǎn)的距離之和等于4.

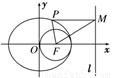
(1)求橢圓和圓的標(biāo)準(zhǔn)方程；

(2)設(shè)直線l的方程為x＝4，PM⊥l，垂足為M，是否存在點(diǎn)P，使得△FPM為等腰三角形？若存在，求出點(diǎn)P的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．

查看答案和解析>>

如圖，已知橢圓

的焦點(diǎn)和上頂點(diǎn)分別為F₁、F₂、B，我們稱△F₁BF₂為橢圓C的特征三角形．如果兩個(gè)橢圓的特征三角形是相似的，則稱這兩個(gè)橢圓是“相似橢圓”，且三角形的相似比即為橢圓的相似比．
（1）已知橢圓

和

判斷C₂與C₁是否相似，如果相似則求出C₂與C₁的相似比，若不相似請(qǐng)說(shuō)明理由；
（2）寫(xiě)出與橢圓C₁相似且半短軸長(zhǎng)為b的橢圓C_b的方程，并列舉相似橢圓之間的三種性質(zhì)（不需證明）；
（3）已知直線l：y=x+1，在橢圓C_b上是否存在兩點(diǎn)M、N關(guān)于直線l對(duì)稱，若存在，則求出函數(shù)f（b）=|MN|的解析式．

查看答案和解析>>

如圖，F(xiàn)是橢圓的右焦點(diǎn)，以點(diǎn)F為圓心的圓過(guò)原點(diǎn)O和橢圓的右頂點(diǎn)，設(shè)P是橢圓上的動(dòng)點(diǎn)，P到橢圓兩焦點(diǎn)的距離之和等于4.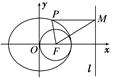

(1)求橢圓和圓的標(biāo)準(zhǔn)方程；
(2)設(shè)直線l的方程為x＝4，PM⊥l，垂足為M，是否存在點(diǎn)P，使得△FPM為等腰三角形？若存在，求出點(diǎn)P的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．

查看答案和解析>>

1.A 2.B 3.C 4.C 5.A 6.C 7.D 8.D 9.A 10.C

11.80 12.30 13.c 14. 15. .

三、解答題

16．解：（1）(ka+b)²=3(a－kb)² k²++2ka?b=3(1+k²－2ka?b)

∴a?b= 當(dāng)k=1時(shí)取等號(hào). （6分）

（2）a?b=

∴時(shí)，a?b=取最大值1. （12分）

17．解：（1）由已知有x_n₊₁－1=2(x_n－1)

∴{x_n－1}是以1為首項(xiàng)以2為公比的等比數(shù)列，又x₁=2.

∴x_n－1=2ⁿ^－1 ∴x_n=1+2ⁿ^－1(n∈N*) （6分）

（2）由

又當(dāng)n∈N*時(shí)，x_n≥2故點(diǎn)（x_n，y_n）在射線x+y=3（x_n≥2）上。（12分）

18．解：（1）記乙勝為事件A，則P（A）=


（2）解法一：由題意：(x，y)=（1，4）或（1，3）或（1，2）或（1，1）或（2，3）或（2，2）或（2，1）或（3，2）或（3，1）或（4，1）。故當(dāng)x=1，y=4時(shí)，x+2y取最大值9，即x=1， y=4時(shí)乙獲勝的概率最大為.（12分）解法二：令t=x+2y，，（x,y）取值如圖所示，由線性規(guī)劃知識(shí)知x=1,y=4時(shí)，t最大，故x=1，y=4，乙獲勝的概率最大為. （12分） 19．解（1）設(shè)正三棱柱―的側(cè)棱長(zhǎng)為．取中點(diǎn)，連．是正三角形，．又底面側(cè)面，且交線為．側(cè)面．……3分連，則直線與側(cè)面所成的角為．在中，，解得．此正三棱柱的側(cè)棱長(zhǎng)為． ……5分（2）過(guò)作于，連，側(cè)面．為二面角的平面角．…7分在中，，又，．又在中，．故二面角的大小為． ……9分（3）解法1：由（2）可知，平面,平面平面，且交線為，過(guò)作于，則平面．……11分在中，．為中點(diǎn)，點(diǎn)到平面的距離為． ………… 13 20．解： 21．解：（1） ∴，故橢圓Q_n的焦距2c_n≥1. （4分）（2）（i）設(shè)P_n(x_n，y_n)，則同步練習(xí)冊(cè)答案全品作業(yè)本答案同步測(cè)控優(yōu)化設(shè)計(jì)答案長(zhǎng)江作業(yè)本同步練習(xí)冊(cè)答案同步導(dǎo)學(xué)案課時(shí)練答案仁愛(ài)英語(yǔ)同步練習(xí)冊(cè)答案一課一練創(chuàng)新練習(xí)答案時(shí)代新課程答案新編基礎(chǔ)訓(xùn)練答案能力培養(yǎng)與測(cè)試答案更多練習(xí)冊(cè)答案國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) \| 網(wǎng)上有害信息舉報(bào)專區(qū) \| 電信詐騙舉報(bào)專區(qū) \| 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) \| 涉企侵權(quán)舉報(bào)專區(qū) 違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com 版權(quán)聲明：本站所有文章，圖片來(lái)源于網(wǎng)絡(luò)，著作權(quán)及版權(quán)歸原作者所有，轉(zhuǎn)載無(wú)意侵犯版權(quán)，如有侵權(quán)，請(qǐng)作者速來(lái)函告知，我們將盡快處理，聯(lián)系qq：3310059649。 ICP備案序號(hào): 滬ICP備07509807號(hào)-10 鄂公網(wǎng)安備42018502000812號(hào) 感谢您访问我们的网站，您可能还对以下资源感兴趣：亚洲高清精品视频国产日韩欧美激情\| 污污的网站在线免费观看\| www.豆豆成人网.com\| 国产福利不卡视频\| 日韩免费视频一区\| 亚洲资源在线看\| 女同性αv亚洲女同志\| 国产精选久久久\| 国产精品黄色片\| 开心九九激情九九欧美日韩精美视频电影 \| 久久久精品综合\| 亚洲男人天堂视频\| 中文字幕免费在线不卡\| 成人免费视频网站入口::\| 国产福利小视频在线观看\| 亚洲啊v在线观看\| 午夜精品福利久久久\| 日本三级韩国三级久久\| 一路向西2在线观看\| 国产精品特级毛片一区二区三区\| 久久电影天堂\| 99视频超级精品\| 丝袜情趣国产精品\| 国产日韩欧美精品在线观看\| 欧美日韩亚洲综合一区二区三区激情在线\| 欧美一区二区免费在线观看\| 最新在线观看av网站\| 欧美一级二级三级视频\| 国产精品区一区二区三区\| 欧美日本精品在线\| 精品视频一区二区在线\| 国产理论片在线观看\| 999久久久精品一区二区\| 国产欧美精品一区二区色综合\| 美女久久久久久久久久久\| 国产精品沙发午睡系列\| 99久久精品国产色欲\| 在线精品视频一区\| 久久综合中文\| 日韩一级视频免费观看在线\| 欧美一区二区三区四区夜夜大片 \| 国产十六处破外女视频\| xxxx视频在线\| 韩国av一区二区\| 国产午夜精品视频\| 99热在线这里只有精品\| 亚洲AV无码成人片在线观看 \| 一区二区三区国产\| 成人福利在线观看\| 亚洲第一综合网\| 国产精品69xx\| 国产成人综合自拍\| 久久婷婷国产麻豆91天堂\| 97视频在线免费播放\| 欧美亚洲精品在线观看\| 日韩精品一区二区三区免费观看 \| 亚洲va欧美va人人爽午夜\| 91久久在线观看\| 777777国产7777777\| 69久成人做爰电影\| 91色porny蝌蚪\| 欧美一区二三区\| 亚洲黄色在线网站\| 伊人春色在线观看\| 国产成人av电影在线\| 欧美久久精品一级黑人c片 \| 国产精品久久久毛片\| 在线国产网址\| 午夜一级在线看亚洲\| 日韩激情av在线免费观看\| 日韩精品视频在线观看视频\| www.av在线.com\| 香蕉视频国产精品\| 日韩精品一区二区三区swag\| 欧美中文字幕在线观看视频\| 欧美视频在线观看一区二区三区\| 亚洲欧洲日韩\| 亚洲国产成人精品一区二区\| 一二三四视频社区在线\| 日本一级淫片免费放\| 国产高清视频一区二区\| 一区二区三区日韩\| 国产伦精品一区二区三区免\| 西西44rtwww国产精品\| 国产伦精品一区二区三区在线播放 \| 91白丝在线\| 91老司机福利在线\| 国产成人免费av电影\| eeuss中文字幕\| 久久影视精品\| 亚洲最大的成人av\| 欧美二区三区在线\| 在线观看毛片网站\| 888久久久\| 亚洲经典中文字幕\| 色综合色综合色综合色综合\| 伊人免费在线\| 国产成人精品亚洲日本在线桃色\| 欧美一级大胆视频\| 人与动物性xxxx\| 深夜福利一区二区三区\| 福利视频一区二区\| 中文字幕一区综合\| 亚洲欧美激情另类\| 午夜一区二区三区不卡视频\| 精品国产欧美成人夜夜嗨\| 成年人小视频在线观看\| 原纱央莉成人av片\| 亚洲精品中文在线观看\| 日韩av电影免费观看\| 亚洲av无码国产精品永久一区 \| 日韩一区二区三区国产\| 日本一区二区在线免费观看\| 偷拍视频一区二区三区\| 一区二区三区美女毛片\| 茄子视频成人在线观看 \| a在线播放不卡\| 成人av色在线观看\| 欧美日韩一区二区三区\| 亚洲成人日韩\| 在线亚洲男人天堂\| 免费看污黄网站在线观看\| 欧美影视资讯\| 欧美日韩国产在线播放\| 大荫蒂性生交片\| 高清在线观看av\| 91免费看`日韩一区二区\| 亚洲自拍偷拍一区\| 一级全黄少妇性色生活片\| 在线免费观看欧美\| 欧美人与物videos\| 538精品在线视频\| 网红女主播少妇精品视频\| 精品少妇一区二区三区免费观看 \| 四虎影院在线免费播放\| 一本到12不卡视频在线dvd\| 在线亚洲国产精品网\| 日本美女xxx\| 欧美激情影院\| 亚洲国内高清视频\| 三级视频网站在线观看\| 亚洲影视资源\| 717成人午夜免费福利电影\| www.久久久精品\| 美女100%一区\| 日韩欧美国产黄色\| 久久久久久久久久福利\| 女人黄色免费在线观看\| 亚洲国产一二三\| 免费拍拍拍网站\| 日皮视频在线观看\| 亚洲国产综合色\| 北条麻妃在线视频观看\| 欧美videossex另类\| 婷婷国产v国产偷v亚洲高清\| 欧美日韩亚洲一区\| 色噜噜狠狠狠综合欧洲色8\| 亚洲影院久久精品\| 日韩中文字幕在线视频观看 \| 日韩最新av在线\| 欧美性x x x\| 欧美第一精品\| 成年无码av片在线\| 日本免费一二三区\| 亚洲第一在线\| 国产精品av在线\| 6—12呦国产精品\| 久久er99精品\| 国产精品对白刺激久久久\| 熟妇高潮一区二区高潮\| 99视频精品全部免费在线\| 欧美另类一区\| 国产特黄在线\| 亚洲精品欧美在线\| 北条麻妃在线观看\| 欧美日韩激情电影\| 日韩久久久精品\| 国产一二三四五区\| 欧美三级伦理在线\| 欧美激情亚洲自拍\| 蜜臀尤物一区二区三区直播\| 青青草国产成人av片免费\| 91九色在线观看\| 欧美写真视频一区\| 国产精品久久久一区麻豆最新章节\| 91视频成人免费\| 成人黄色动漫\| 制服丝袜在线91\| 国产免费看av\| 久久久五月天\| 国产精品成人va在线观看\| 国产成人精品免费看视频\| 波多野结衣中文字幕一区二区三区\| 日韩精品久久久免费观看\| 免费大片黄在线\| 色婷婷一区二区三区四区\| 男人操女人下面视频\| 鲁大师精品99久久久\| 日韩视频在线观看免费\| 国产97色在线\| 夜夜添无码一区二区三区\| free性m.freesex欧美\| 欧美美女直播网站\| 毛茸茸多毛bbb毛多视频\| 欧美激情国产在线\| 国产极品jizzhd欧美\| 免费观看a视频\| 国产精品久久三\| 东京热加勒比无码少妇\| 国产精品毛片无码\| 日韩在线一区二区三区免费视频\| 国产成人一区二区三区影院在线\| 秋霞av亚洲一区二区三\| 欧美一区二区三区四区夜夜大片 \| 亚洲精品www久久久\| 中文字幕av久久爽av\| 亚洲欧美视频\| 精品久久久久久中文字幕动漫\| jizz在线观看视频\| 国产福利91精品一区二区三区\| 涩涩涩999\| av中文字幕在线观看第一页\| 日韩欧美久久久\| 欧美一区二区三区爽爽爽\| 久久在线精品\| 日本不卡一区二区三区在线观看\| 182tv在线播放\| 91麻豆精品国产91久久久久久久久\| 调教驯服丰满美艳麻麻在线视频\| 亚洲精品九九\| 久久国产日韩欧美\| 金瓶狂野欧美性猛交xxxx \| 欧美亚洲另类小说\| 99精品视频在线免费观看\| 久无码久无码av无码\| 伊人亚洲精品\| 欧美精品在线观看\| 亚洲欧美国产高清va在线播放\| 国产精品国产三级国产普通话三级 \| 夜夜嗨av一区二区三区免费区\| 国产在线观看黄色\| a亚洲天堂av\| 日韩中文字幕二区\| 免费av一区\| 国产精品一香蕉国产线看观看\| 国产在线三区\| 3d动漫精品啪啪一区二区竹菊\| 最新黄色av网址\| 国产一区二区精品久久\| 欧美人成在线观看\| 国产精品久久久久av蜜臀\| 97超碰国产精品女人人人爽 \| 亚洲无限av看\| 国产精品无码一区二区桃花视频 \| 欧美国产激情二区三区\| 一区二区免费av\| 香蕉视频国产精品\| 精品蜜桃传媒\| 成人av观看\| 久久躁狠狠躁夜夜爽\| 内射无码专区久久亚洲\| 午夜欧美2019年伦理\| 欧美大波大乳巨大乳\| 免费观看久久久4p\| 日本手机在线视频\| 香蕉久久夜色精品国产使用方法 \| 亚洲九九视频\| 久久一区二区三区av\| 肉色欧美久久久久久久免费看\| 丝袜情趣国产精品\| 中出福利视频\| 欧美曰成人黄网\| 国产一级二级三级视频\| 91免费看片在线观看\| www.色就是色.com\| 国产综合精品\| 永久免费精品视频网站\| 综合激情网...\| 国产色综合天天综合网 \| 色yeye免费人成网站在线观看\| 亚洲欧美制服丝袜\| 欧美天堂在线视频\| 欧美午夜精品久久久\| 国产精品久久久免费视频\| 日本一区二区视频在线观看\| 性高潮免费视频\| 日韩精品三区四区\| 精品久久一二三\| 欧美成人milf\| 亚洲一区二区三区精品视频\| 亚洲专区\| 91手机视频在线观看\| 九九精品调教\| 久久综合久久美利坚合众国\| 香蕉av一区\| 精品国产区一区\| 国产av无码专区亚洲av麻豆\| 午夜精品久久久久久久久久\| 精品国产欧美日韩不卡在线观看 \| 午夜精品在线视频\| 麻豆tv入口在线看\| 日韩在线小视频\| 国产在线资源\| 亚洲天堂一区二区三区\| 最新理论片影院\| 精品欧美久久久\| 亚洲国产精品欧美久久\| 欧美日韩精品久久久\| 在线观看毛片视频\| 在线免费不卡视频\| 欧美日韩一区二区三区\| 欧美日韩国产精品一区二区三区四区\| 男女羞羞免费视频\| 国产精品久久久久久久久动漫\| 人妻aⅴ无码一区二区三区\| 91原创在线视频\| 西西444www无码大胆\| 91免费精品国自产拍在线不卡\| 亚洲色图14p\| av电影天堂一区二区在线\| 亚洲永久无码7777kkk\| 成人免费观看av\| 国产精品一级黄片\| 成人av中文字幕\| 中国美女乱淫免费看视频\| 不卡的av电影\| 在哪里可以看毛片\| 久久综合九色综合久久久精品综合\| 国产老熟女伦老熟妇露脸\| 成人一区二区三区视频\| 水蜜桃av无码\| av电影天堂一区二区在线\| 精品人伦一区二区三电影\| 久久天堂av综合合色蜜桃网\| 久久久久久久久福利\| 日本一区二区视频在线\| 波多野结衣喷潮\| 亚洲精品视频在线\| 天天操天天干视频\| 欧美午夜久久久\| 中文字字幕在线中文乱码\| 欧美日韩一区二区三区在线\| h狠狠躁死你h高h\| 精品国产乱码久久久久久浪潮\| 啦啦啦啦免费高清视频在线观看1\| 日韩成人久久久\| 韩国福利在线\| 欧美日本中文字幕\| h片在线观看下载\| 国产精自产拍久久久久久蜜\| 色999久久久精品人人澡69\| 国产精品一区二区三区四区五区\| 国产主播性色av福利精品一区\| 日韩激情视频\| 影视亚洲一区二区三区\| 久久久999视频\| 日韩精品五月天\| 捆绑凌虐一区二区三区\| 久久老女人爱爱\| 国产精品999久久久\| 欧美性极品xxxx娇小\| 国产三级第一页\| 日韩av影视在线\| 亚洲麻豆精品\| 日本最新高清不卡中文字幕\| a成人v在线\| 欧美国产综合视频\| 97视频热人人精品免费\| 免费黄色福利视频\| 国精产品一区一区三区mba桃花\| 欧美精品黑人猛交高潮\| 国产精品久久久久7777按摩\| 国产又黄又粗又爽\| 欧美精品久久99久久在免费线 \| 免费看成年人视频在线观看\| 色一情一乱一区二区\| 黄色污污视频在线观看\| 91精品免费看\| 亚洲激情播播\| 香港三级韩国三级日本三级\| 蜜桃av一区二区三区电影\| 成人h动漫精品一区\| 亚洲免费av观看\| 一级久久久久久久\| 亚洲女人天堂av\| 欧美黄色视屏\| av一本久道久久波多野结衣\| 国产videos久久\| 国产av无码专区亚洲精品\| 国产成人av电影在线观看\| 东方av正在进入\| 欧洲亚洲精品在线\| 在线观看免费网站\| 久久欧美在线电影\| 91成人福利社区\| 亚洲AV无码成人精品一区\| 老司机免费视频久久\| 久久久久久九九九九九\| 一区av在线播放\| 蜜臀久久久久久999\|

練習(xí)冊(cè)

高中

初中

小學(xué)