題目列表(包括答案和解析)
C．選修4-4：坐標(biāo)系與參數(shù)方程
在極坐標(biāo)系下，已知圓O：
和直線
，
（1）求圓O和直線
的直角坐標(biāo)方程；（2）當(dāng)
時，求直線與圓O公共點的一個極坐標(biāo).
D．選修4-5：不等式證明選講
對于任意實數(shù)
和
，不等式
恒成立，試求實數(shù)
的取值范圍．
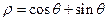和直線
，
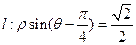的直角坐標(biāo)方程；（2）當(dāng)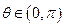
時，求直線與圓O公共點的一個極坐標(biāo).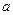
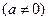和
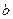，不等式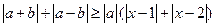
恒成立，試求實數(shù)
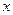的取值范圍．C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B錯；
＋
＝
＝
≥4，故A錯；由基本不等式得
≤
＝
，即
＋
≤
，故C正確；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D錯．故選C.
．定義域為R的函數(shù)
滿足
，且當(dāng)
時，
，則當(dāng)
時，
的最小值為（ ）
（A）
（B）
（C）
（D）
．過點
作圓
的弦，其中弦長為整數(shù)的共有 （ ）
A.16條 B. 17條 C. 32條 D. 34條
一、選擇題：
CADDB ADBBA CD
二、填空題
（13）2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image281.gif)
; （14）8; （15）2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image283.gif)
; （16）2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image285.gif)
.
三、解答題
（17）解：將圓C的方程2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image182.gif)
配方得標(biāo)準(zhǔn)方程為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image287.gif)
，
則此圓的圓心為（0 , 4），半徑為2.
(Ⅰ) 若直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image137.gif)
與圓C相切，則有2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image289.gif)
. 解得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image291.gif)
. ………………6分
(Ⅱ) 解：過圓心C作CD⊥AB，則根據(jù)題意和圓的性質(zhì)，得
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image293.gif)
解得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image295.gif)
.
∴直線的方程是2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image297.gif)
和2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image299.gif)
. ………………12分
（18）解:(Ⅰ)由題意知此平面區(qū)域表示的是以2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image301.gif)
構(gòu)成的三角形及其內(nèi)部,且△2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image303.gif)
是直角三角形, 所以覆蓋它的且面積最小的圓是其外接圓,故圓心是(2,1),半徑是2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image305.gif)
,
所以圓2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image193.gif)
的方程是2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image308.gif)
. ………………6分
(Ⅱ)設(shè)直線的方程是:2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image310.gif)
.
因為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image312.gif)
,所以圓心到直線的距離是2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image314.gif)
, 即2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image316.gif)
.
解得:2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image318.gif)
. ………………………………11分
所以直線的方程是2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image320.gif)
. ………………12分
（19）解：設(shè)過點T(3,0)的直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image201.gif)
交拋物線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image322.gif)
于點A2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image324.gif)
、B2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image326.gif)
.
（Ⅰ）當(dāng)直線的鈄率不存在時,直線的方程為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image328.gif)
,
此時, 直線與拋物線相交于點A(3,2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image330.gif)
)（）.B(3,－)，∴2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image333.gif)
=3. …….............4分
（Ⅱ）當(dāng)直線的鈄率存在時,設(shè)直線的方程為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image335.gif)
，
其中2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image337.gif)
，由2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image339.gif)
得 2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image341.gif)
.
…………………….….6分
又 ∵ 2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image343.gif)
， ∴2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image345.gif)
，
………………………………….10分
綜上所述，命題“若直線過點T(3,0)，則=3” 是真命題. ………………….12分
（20）解：（Ⅰ）由2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image215.gif)
知2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image213.gif)
是2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image349.gif)
的中點，
設(shè)A、B兩點的坐標(biāo)分別為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image351.gif)
由2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image353.gif)
.
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image355.gif)
，
∴點的坐標(biāo)為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image357.gif)
.
…………………………4分
又點在直線上， 2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image360.gif)
.
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image362.gif)
， 2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image364.gif)
………………6分
（Ⅱ）由（Ⅰ）知2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image366.gif)
，不妨設(shè)橢圓的一個焦點坐標(biāo)為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image368.gif)
，
設(shè)關(guān)于直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image372.gif)
上的對稱點為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image374.gif)
，
則有2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image376.gif)
. ………………10分
由已知2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image378.gif)
.
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image380.gif)
，∴所求的橢圓的方程為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image382.gif)
. ………………12分
（21）解：（Ⅰ）2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image384.gif)
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image386.gif)
，即2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image388.gif)
；
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image390.gif)
，即2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image392.gif)
.
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image394.gif)
. ……………………………………………4分
（Ⅱ）設(shè)直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image396.gif)
的方程為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image398.gif)
，
直線與雙曲線交于2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image401.gif)
，不妨設(shè)2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image403.gif)
且2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image405.gif)
，
直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image407.gif)
與雙曲線交于2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image409.gif)
.
由2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image411.gif)
得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image413.gif)
.
令2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image415.gif)
得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image417.gif)
，此式恒成立.
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image419.gif)
，2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image421.gif)
. ………………6分
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image423.gif)
而2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image425.gif)
=2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image427.gif)
.
∴直線與雙曲線交于兩支上的兩點；
同理直線與雙曲線交于兩支上的兩點，
則2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image431.gif)
……………………8分
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image433.gif)
=2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image435.gif)
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image437.gif)
=2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image439.gif)
. ……………………10分
令2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image441.gif)
則2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image443.gif)
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image445.gif)
在（1，2）遞增.
又2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image447.gif)
，
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image449.gif)
.
………………………………………12分
（22）解：（Ⅰ）直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image451.gif)
的法向量2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image453.gif)
， 的方程：2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image456.gif)
，
即為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image458.gif)
. ………………………2分
直線2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image460.gif)
的法向量2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image462.gif)
，的方程為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image465.gif)
，
即為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image467.gif)
.
………………………4分
（Ⅱ）2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image469.gif)
. ………………………6分
設(shè)點2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image260.gif)
的坐標(biāo)為2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image472.gif)
，由2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image474.gif)
，得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image476.gif)
.…………8分
由橢圓的定義的知，存在兩個定點2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image478.gif)
使得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image480.gif)
恒為定值4，此時兩個定點為橢圓的兩個焦點. ………………………10分
（Ⅲ）設(shè)2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image483.gif)
，2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image485.gif)
，則2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image487.gif)
，2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image489.gif)
，
由2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image491.gif)
，得2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image493.gif)
. ………………………12分
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image495.gif)
；
當(dāng)且僅當(dāng)2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image497.gif)
或2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image499.gif)
時，2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image501.gif)
取最小值2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image503.gif)
.
2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image505.gif)
，故2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image507.gif)
與2009年高考沖刺專題訓(xùn)練（五）解析幾何測試題（理科）.files/image509.gif)
平行.
………………………14分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com