
題目列表(包括答案和解析)
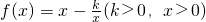 ,則f(x2+1)與f(x)的大小關系為________.
,則f(x2+1)與f(x)的大小關系為________.A.f(x)>g(x)
B.f(x)<g(x)
C.f(x)=g(x)
D.大小關系不能確定
A.f(x)>g(x)
B.f(x)<g(x)
C.f(x)=g(x)
D.大小關系不能確定
已知函數 的圖象過坐標原點O,且在點
的圖象過坐標原點O,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實數 的值;
的值;
(Ⅱ)求 在區間
在區間 上的最大值;
上的最大值;
(Ⅲ)對任意給定的正實數 ,曲線
,曲線 上是否存在兩點P、Q,使得
上是否存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上?說明理由.
軸上?說明理由.
【解析】第一問當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問當 時,
時, ,令
,令 得
得 ,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
第三問假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
(Ⅰ)當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當 時,
時, ,令
,令 得
得
當 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當 時,
時,  .當
.當 時,
時,  ,
, 最大值為0;
最大值為0;
當 時,
時,  在
在 上單調遞增。∴
上單調遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為2;
上的最大值為2;
當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無解,因此
,而此方程無解,因此 。此時
。此時 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調遞增, ∵
上單調遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對任意給定的正實數 ,曲線
,曲線 上存在兩點P、Q,使得
上存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上
軸上
一、選擇題 ACCBC BBCCD
二、填空題: ,
, ,
, ,
, ,
, ,
, ,①②④
,①②④
18(Ⅰ)由題意“ 且
且 ”表示“答完
”表示“答完 題,第一題答對,第二題答錯;或第一題答對,第二題也答對” 此時概率
題,第一題答對,第二題答錯;或第一題答對,第二題也答對” 此時概率
 …6分
…6分
(Ⅱ)P( )=
)= =
= , P(
, P( )=
)= =
= ,………9分
,………9分

-3
-1
1
3





P( )=
)= =
= ,
P(
,
P( )=
)= =
=
∴ 的分布列為
的分布列為
12分
∴ ……14分
……14分
19解:(Ⅰ) 連接 交
交 于點
于點 ,連接
,連接 .
.
在 中,
中,
 分別為
分別為 中點,
中點,
 .
.

 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 . …………(6分)
. …………(6分)
(Ⅱ) 法一:過 作
作 于
于 ,由三垂線定理得
,由三垂線定理得 ,
,
故∠ 為二面角
為二面角 的平面角. ……………………………………(9分)
的平面角. ……………………………………(9分)
令 ,則
,則 ,又
,又 ,
,
在 △
△ 中,
中, ,
,
解得 。
。

 當
當 時,二面角
時,二面角 的正弦值為
的正弦值為 . ………………(14分)
. ………………(14分)
法二:設 ,取
,取 中點
中點 ,連接
,連接 ,
,
以 為坐標原點建立空間直角坐標系,如右圖所示:
為坐標原點建立空間直角坐標系,如右圖所示:
則 ,
,
則 .
.
設平面 的法向量為
的法向量為 ,平面
,平面 的法向量為
的法向量為 ,
,
則有 ,
, ,即
,即 ,
, ,
,
設 ,則
,則 ,
,



 ,解得
,解得 .
.
 即當
即當 時,二面角
時,二面角 的正弦值為
的正弦值為 . …………………(14分)
. …………………(14分)
20.(1)  ;
;
(2)軌跡方程為 (
( )
)
(1)當 時,軌跡方程為
時,軌跡方程為 (
( ),表示拋物線弧段。
),表示拋物線弧段。
(2)當 時,軌跡方程為
時,軌跡方程為 ,
,
A)當 表示橢圓弧段; B)當
表示橢圓弧段; B)當 時表示雙曲線弧段。
時表示雙曲線弧段。
21.
Ⅰ) …………(2分)
…………(2分)
令 ,則
,則
當 時,
時, ;當
;當 時
時 
故有極大值 …………(4分)
…………(4分)
Ⅱ)∵ =a+
=a+ ,x∈(0,e),
,x∈(0,e), ∈[
∈[ ,+∞
,+∞
(1)若a≥- ,則
,則 ≥0,從而f(x)在(0,e)上增函數.
≥0,從而f(x)在(0,e)上增函數.
∴f(x)max =f(e)=ae+1≥0.不合題意. …………………………………7分
(2)若a<- ,
,  >
> a+
a+ >0,即0<x<-
>0,即0<x<-
由
 a+
a+ <0,即-
<0,即- <x≤e.
<x≤e.
∴f(x) =f(-
=f(- )=-1+ln(-
)=-1+ln(- ).
).
令-1+ln(- )=-3,則ln(-
)=-3,則ln(- )=-2.∴-
)=-2.∴- =e
=e ,
,
即a=-e2. ∵-e2<- ,∴a=-e2為所求. ……………………………10分
,∴a=-e2為所求. ……………………………10分
Ⅲ)由Ⅰ)結論, =f(1)=-1.∴f(x)=-x+lnx≤-1,從而lnx≤x-1.
=f(1)=-1.∴f(x)=-x+lnx≤-1,從而lnx≤x-1.
令g(x)=|f(x)|- -
- =x-lnx-
=x-lnx- -
- =x-(1+
=x-(1+ )lnx-
)lnx- ……12分
……12分
(1)當0<x<2時,有g(x)≥x-(1+ )(x-1)-
)(x-1)- =
= -
- >0.
>0.
(2)當x≥2時,g′(x)=1-[(- )lnx+(1+
)lnx+(1+ )?
)? ]=
]=
= .
.
∴g(x)在[2,+∞ 上增函數,∴g(x)≥g(2)=
上增函數,∴g(x)≥g(2)=
綜合(1)、(2)知,當x>0時,g(x)>0,即|f(x)|> .
.
故原方程沒有實解. ………………………………16分
22.證明:(I)
①當 , …………2分
, …………2分
②假設 ,
,
則 時不等式也成立,
時不等式也成立, …………4分
…………4分
(II)由 ,
,
由
…………5分

又 …………7分
…………7分
 …………8分
…………8分
(III) ,
,
 , …………10分
, …………10分

 的等比數列,…………12分
的等比數列,…………12分

 …………14分
…………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com