題目列表(包括答案和解析)
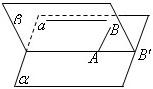13、求證：若一直線與一個平面平行，則過平面內的一點且與這條直線平行的直線必在此平面內．| 2n-1 |
| 2n+1 |
| n |
| n+1 |
1、
； 2、24x2 3、
4、－1或3
5、
6、2n 7、
8、8π
9、如①y＝0，－2x－1 ②x＝0，1－2x
③y＝x，
等 10、① 11、
12、B 13、A 14、D 15、A
16、解：取BC中點E，連接B1E，得B1ECD為平行四邊形
∵B1E∥CD
∴∠AB1E為異面直線AB1與CD所成的角. (4分)
在△ABC中，BC＝4
連接AE，在△AB1E中，AB1＝4，AE＝2，B1E＝2
，
(7分)
則cos∠AB1E＝
＝
＝
(10分)
∴異面直線AB1與CD所成角的大小為300. (12分)
17、解：(1) 由(2－x) (x＋1)＞0，得－1＜x＜2 即A＝(－1，2) (6分)
(2) 由(x－m－2)(x－m)＞0，得B＝(－∞，m)∪(m＋2，＋∞) (10分)
∵A
B ∴m≥2或m＋2≤－1，即m≥2或m≤－3
故當BA時，實數a的取值范圍是(－∞，－3]∪[2，＋∞)
(14分)
18、解：在△ABC中，BD＝400，∠ABD＝1200，
∵∠ADB＝200 ∴∠DAB＝400
∵
＝
(2分)
∴
＝
，得AD≈538.9 (7分)
在△ADC中，DC＝800，∠ADC＝1600
∴AC2＝AD2＋DC2－2 AD•DC•cos∠ADC (9分)
＝538.92＋8002－2×538.9×800×cos1600
＝1740653.8
得AC≈1319（米） (14分)
則索道AC長約為
19、解：（1）
，即
但
，所以
（若答案寫成，扣一分）
(4分)
（2）任取
，則
，
， (6分)
所以
，
當且僅當
時等號成立，則g(x)∈M.
(10分)
（3）設
，則
，且m＋n＝1.
由已知：函數
滿足
得
，即
，則
(14分)
當且僅當，即
，即m＝n＝－1時，m＋n有最大值為－2. (16分)
21、解：（1）
(2分)
則
(4分)
（2）
，
∵
∴
∴
(
)，知
是周期為3的數列 (6分)
則
＝
(10分)
（3）
(14分)
所以
，即
(18分)
上海市奉賢區2008年高三數學聯考試卷(理)
一、填空題（本大題滿分55分）本大題共有11題，只要求直接填寫結果，每個空格填對得5分，否則一律得零分．
21.設A＝
，B＝
，則A∩B＝_________________.
22.若
＝3，則x＝_________________.
23.函數
的反函數
_________________.
24.已知
＝(m－2，－3)，
＝(－1，m)，若∥，則m＝_________________.
25.已知復數w滿足
(i為虛數單位），則|
|＝_________________.
26.等差數列
的公差不為零，
. 若
成等比數列，則
__________.
27.已知
，且
是第四象限的角，則
＝_________________.
28.已知圓錐的母線與底面所成角為600，高為3，則圓錐的側面積為_________________.
29.請將下面不完整的命題補充完整，并使之成為真命題：若函數f(x)＝2
－1的圖像與g(x)的圖像關于直線_____________對稱，則g(x)＝_________________.
（注：填上你認為可以成為真命題的一種情形即可）
30.對于函數f(x)＝x?sinx，給出下列三個命題：①f(x)是偶函數；②f(x)是周期函數；③f(x) 在區間[0，π]上的最大值為
.正確的是_______________（寫出所有真命題的序號）.
31.正方體中，連接相鄰兩個面的中心的連線可以構成一個美麗的幾何體.若正方體的邊長為1，則這個美麗的幾何體的體積為_______________.
二. 選擇題（本大題滿分20分）本大題共有4 題，每題都給出代號為A、B、C、D的四個結論，其中有且只有一個結論是正確的，必須把正確結論的代號寫在題后的圓括號內，選對得5分，不選、選錯或者選出的代號超過一個，一律得零分．
32.下列函數中，奇函數是（ ）
(A) y＝x2－1 (B) y＝x3＋x (C) y＝2 (D) y＝log3x
33. 設x1、x2∈R，則“x1＞1且x2＞
(A) 充分不必要 (B) 必要不充分 (C) 充要 (D) 不充分不必要
34.設向量＝(－2，1)，＝(λ，－1) (λ∈R)，若、的夾角為鈍角，則λ的取值范圍是（
）
(A) (－∞, －
) (B) (－, ＋∞) (C) (, ＋∞) (D) (－, 2)∪(2, ＋∞)
35.將1，2，…，9這9個數隨機分給甲、乙、丙三人，每人三個數，則每人手中的三個數都能構成等差數列的概率為（ ）
(A) 
(B)
(C)
(D)
三. 解答題（本大題滿分75分）本大題共有5題，解答下列各題必須寫出必要的步驟．
36. （本題滿分12分）
在直三棱柱
中，已知AB＝AC＝AA1＝4，∠BAC＝900，D為B
解：
37. （本題滿分14分.第一小題6分，第2小題8分.）
記函數f(x)＝
的定義域為A，g(x)＝log3[(x－m－2)(x－m)]的定義域為B.
(1)求A；(2)若AB，求實數m的取值范圍.
解：
38. （本題滿分15分）
如圖所示，南山上原有一條筆直的山路BC，現在又新架設了一條索道AC.小李在山腳B處看索道AC，發現張角∠ABC＝1200；從B處攀登
解：
39. （本題滿分16分.第一小題4分，第2小題6分，第3小題6分.）
我們將具有下列性質的所有函數組成集合M：函數
，對任意
均滿足，當且僅當時等號成立.
（4） 若定義在(0，＋∞)上的函數
∈M，試比較
與
大小.
（5） 給定兩個函數：
，
.
證明：
.
（6） 試利用（2）的結論解決下列問題：若實數m、n滿足
，求m＋n的最大值.
解：
40. （本題滿分18分.第1小題4分，第2小題6分，第3小題8分.）
我們規定：對于任意實數
，若存在數列和實數
，使得
，則稱數可以表示成
進制形式，簡記為：
。如：
，則表示A是一個2進制形式的數，且
＝5.
（1）已知
（其中
，試將m表示成進制的簡記形式.
（2）若數列滿足，
，
，是否存在實常數p和q，對于任意的，
總成立？若存在，求出p和q；若不存在，說明理由.
（3）若常數
滿足
且
，
，求
.
解：
奉賢區2008年高三數學聯考試卷(理)參考答案
1、； 2、2或－3 3、
4、－1或3
5、
6、2n 7、
8、6π
9、如①y＝0，－2x＋1；②x＝0，(
)x－1；③y＝x，log2(x＋1)等 10、① 11、
12、B 13、A 14、D 15、A
16、解法一：取BC中點E，連接B1E，得B1ECD為平行四邊形
∵B1E∥CD
∴∠AB1E為異面直線AB1與CD所成的角. (4分)
在△ABC中，BC＝4
連接AE，在△AB1E中，AB1＝4，AE＝2，B1E＝2，
(7分)
則cos∠AB1E＝
＝＝
(10分)
∴異面直線AB1與CD所成角的大小為300. (12分)
解法二：以A為坐標原點，分別以AB、AC、AA1所在直線為
軸、
軸、
軸，建立空間直角坐標系. (2分)
則A(0，0，0)，B1(4，0，4)，C(0，4，0)，D(2，2，4)
得 
＝(4，0，4)，
＝(2，－2，4) (6分)
設與的夾角為
則
＝
(10分)
∴與的夾角大小為300
即異面直線
與
所成角的大小為300. (12分)
17、解：(1) 
－2≥0，得
≤0，－1＜x≤2 即A＝
－1，2] (6分)
(2) 由(x－m－2)(x－m)＞0，得B＝(－∞，m)∪(m＋2，＋∞) (10分)
∵AB ∴m＞2或m＋2≤－1，即m＞2或m≤－3
故當BA時，實數a的取值范圍是(－∞，－3]∪(2，＋∞).
(14分)
18、解：在△ABC中，BD＝400，∠ABD＝1200
∵∠ADB＝200 ∴∠DAB＝400
∵＝
(2分)
∴＝，得AD≈538.9 (7分)
在△ADC中，DC＝800，∠ADC＝1600
∴AC2＝AD2＋DC2－2 AD•DC•cos∠ADC (9分)
＝538.92＋8002－2×538.9×800×cos1600
＝1740653.8
得AC≈1319（米） (14分)
則索道AC長約為
19、解：（1）
，即
但，所以
（若答案寫成，扣一分）
(4分)
（2）① 對于，取
，則
所以
，
. (6分)
②對于任取
，則
∵ 
，而函數是增函數
∴ 
，即
則
，即
.
(10分)
（3）設，則，且m＋n＝1.
由（2）知：函數
滿足
，
得，即，則 (14分)
當且僅當，即，即m＝n＝－1時，m＋n有最大值為－2. (16分)
20、解：（1）
(1分)
則
(3分)
（2）
∵ ∴
∴()，知是周期為3的數列 (6分)
假設存在實常數p和q，對于任意的，總成立，則：
＝
∴ 
.
即存在實常數，對于任意的，
總成立 (10分)
（3）
(14分)
∴ ，即 (18分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com