題目列表(包括答案和解析)
（本小題滿分13分，（I）小問6分，（II）小問7分）
某市公租房的房源位于A、B、C三個片區，設每位申請人只申請其中一個片區的房源，且申請其中任一個片區的房源是等可能的，求該市的任4位申請人中：
（I）沒有人申請A片區房源的概率；
（II）每個片區的房源都有人申請的概率。
（本小題滿分13分）
某研究性學習小組對春季晝夜溫差大小與某花卉種子發芽多少之間的關系進行研究，他們分別記錄了3月1日至3月5日的每天晝夜溫差與實驗室每天每100顆種子浸泡后的發芽數，得到如下資料：
|
日期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
|
溫差x（oC） |
10 |
11 |
13 |
12 |
8 |
|
發芽數y（顆） |
23 |
25 |
30 |
26 |
16 |
（I）從3月1日至3月5日中任選2天，記發芽的種子數分別為m，n，求事件“m，n均小于25”的概率；
（II）請根據3月2日至3月4日的數據，求出y關于x的線性回歸方程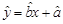
；
（III）若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2顆，則認為得到的線性回歸方程是可靠的，試問（II）所得的線性回歸方程是否可靠？
（參考公式：回歸直線方程式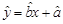，其中
）
（本小題滿分13分）經過市場調查發現，某種產品投放市場的100天中，前40天其價格直線上升，而后60天其價格則呈直線下降趨勢.現抽取其中4天的價格如下表所示:
| 時間(天) | 第8天 | 第32天 | 第70天 | 第90天 |
| 價格(千元) | 24 | 30 | 17 | 7 |
⑴寫出投放市場的第
天的價格關于時間的函數表達式.
⑵若銷售量
與時間(天)的函數關系式是
(1≤x≤100且
)問該產品投放市場第幾天時，日銷售額最大，最大值是多少？
（本小題滿分13分。（Ⅰ）小問5分（Ⅱ）小問8分.）
某市公租房房屋位于A.B.C三個地區，設每位申請人只申請其中一個片區的房屋，且申請其中任一個片區的房屋是等可能的，求該市的任4位申請人中:
（Ⅰ）若有2人申請A片區房屋的概率;
（Ⅱ）申請的房屋在片區的個數的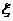
分布列與期望。
（本小題滿分13分）（Ⅰ）小問5分，（Ⅱ）小問8分）
某市公租房的房源位于A，B，C三個片區，設每位申請人只申請其中一個片區的房源，且申請其中任一個片區的房源是等可能的求該市的任4位申請人中：
（Ⅰ）恰有2人申請A片區房源的概率；
（Ⅱ）申請的房源所在片區的個數
的分布列與期望
一、DDBCD CABCA
二、11．1；
12．
； 13．
14．
； 15．
；
16．
三．解答題（本大題共6小題，共76分）
17．解：（1）法一：由題可得
；
法二：由題
，
故
，從而
；
法三：由題
，解得
，
故，從而。
（2）
，令
，
則
，
在
單調遞減，
故
，
從而
的值域為
。
18．解：（1）
的可能取值為0,1,2,3,4，
，
，
，
，
。
因此隨機變量的分布列為下表所示；
0
1
2
3
4
（2）由⑴得：
，
19．法一：（1）連接
，設
，則
。
因為
，所以
，故
，從而
，
故
。
又因為
，
所以
，當且僅當
取等號。
此時
為
邊的中點，
為
邊的中點。
故當為邊的中點時，
的長度最小，其值為
（2）連接
，因為此時
分別為
的中點，
故
，所以
均為直角三角形，
從而
，所以
即為直線
與平面
所成的角。
因為
，所以
即為所求；
（3）因，又
，所以
。
又
，故三棱錐
的表面積為
。
因為三棱錐的體積
，
所以
。
法二：（1）因
，故
。
設
，則
。
所以
，
當且僅當
取等號。此時為邊的中點。
故當為的中點時，的長度最小，其值為；
（2）因，又，所以。
記點到平面的距離為
，
因，故
，解得
。
因
，故
；
（3）同“法一”。
法三：（1）如圖，以
為原點建立空間直角坐標系，設，則
，
所以，當且僅當取等號。
此時為邊的中點，為邊的中點。
故當為邊的中點時，的長度最小，其值為；
（2）設
為面的法向量，因
，
故
。取
，得
。
又因
，故
。
因此
，從而
，
所以；
（3）由題意可設
為三棱錐的內切球球心，
則
，可得
。
與（2）同法可得平面
的一個法向量
，
又
，故
，
解得
。顯然
，故
。
20．解：（1）當
時，
。令
得
，
故當
時
，單調遞增；
當
時
，單調遞減。
所以函數的單調遞增區間為
，
單調遞減區間為
；
（2）法一：因
，故
。
令
，
要使
對滿足
的一切
成立，則
，
解得
；
法二：，故。
由
可解得
。
因為
在
單調遞減，因此
在單調遞增，故
。設
，
則
，因為
，
所以
，從而
在單調遞減，
故
。因此
，即。
（3）因為
，所以
即
對一切
恒成立。
，令
，
則
。因為，所以
，
故
在
單調遞增，有
。
因此
，從而
。
所以
。
21．解：（1）設
，則由題
，
由
得
，故
。
又根據
可得
，
即
，代入可得
，
解得
（舍負）。故的方程為
；
（2）法一：設
，代入得
，
故
，
從而
因此
。
法二：顯然點是拋物線的焦點，點
是其準線
上一點。
設為的中點，過
分別作的垂線，垂足分別為
，
則
。
因此以為直徑的圓與準線相切（于點
）。
若與重合，則
。否則點在
外，因此
。
綜上知。
22．證明：（1）因
，故
。
顯然
，因此數列
是以
為首項，以2為公比的等比數列；
（2）由⑴知
，解得
；
（3）因為
所以
。
又
（當且僅當
時取等號），
故
。
綜上可得
。（亦可用數學歸納法）
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com