
題目列表(包括答案和解析)
設(shè) 若
若 是
是 與
與 的等比中項,則
的等比中項,則 的最小值為( )
的最小值為( )
| A.2 | B. | C.4 | D.8 |
設(shè) 若
若 是
是 與
與 的等比中項,則
的等比中項,則 的最小值為( )
的最小值為( )
A.8
B.4 C.1 D.
設(shè) 若
若 是
是 與
與 的等比中項,則
的等比中項,則 的最小值為
的最小值為
A.1 B. C.
C. D. 4
D. 4
設(shè) 若
若 是
是 與
與 的等比中項,則
的等比中項,則 的最小值為
( )
的最小值為
( )
A. B.
B. C.
C. D.
D.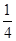
設(shè) 若
若 是
是 與
與 的等比中項,則
的等比中項,則 的最小值為( )
的最小值為( )
A.1 B.2 C.8 D.4
一、DDBCD CABCA
二、11.1;
12.學(xué)理.files/image254.gif) ; 13.
; 13.學(xué)理.files/image256.gif) 14.
14.學(xué)理.files/image258.gif) ; 15.
; 15.學(xué)理.files/image260.gif) ;
;
16.學(xué)理.files/image262.gif)
三.解答題(本大題共6小題,共76分)
17.解:(1)法一:由題可得學(xué)理.files/image264.gif) ;
;
法二:由題學(xué)理.files/image266.gif) ,
,
故學(xué)理.files/image268.gif) ,從而
,從而學(xué)理.files/image270.gif) ;
;
法三:由題學(xué)理.files/image272.gif) ,解得
,解得學(xué)理.files/image274.gif) ,
,
故學(xué)理.files/image268.gif) ,從而
,從而學(xué)理.files/image270.gif) 。
。
(2)學(xué)理.files/image276.gif) ,令
,令學(xué)理.files/image278.gif) ,
,
則學(xué)理.files/image280.gif) ,
,
學(xué)理.files/image282.gif) 在
在學(xué)理.files/image284.gif) 單調(diào)遞減,
單調(diào)遞減,
故學(xué)理.files/image286.gif)
學(xué)理.files/image288.gif) ,
,
從而學(xué)理.files/image083.gif) 的值域為
的值域為學(xué)理.files/image291.gif) 。
。
18.解:(1)學(xué)理.files/image126.gif) 的可能取值為0,1,2,3,4,
的可能取值為0,1,2,3,4,學(xué)理.files/image293.gif) ,
,
學(xué)理.files/image295.gif)
學(xué)理.files/image297.gif) ,
,
學(xué)理.files/image299.gif) ,
,學(xué)理.files/image301.gif) ,
,學(xué)理.files/image303.gif)
學(xué)理.files/image305.gif) 。
。
因此隨機變量學(xué)理.files/image126.gif) 的分布列為下表所示;
的分布列為下表所示;
學(xué)理.files/image126.gif)
0
1
2
3
4
學(xué)理.files/image142.gif)
學(xué)理.files/image308.gif)
學(xué)理.files/image297.gif)
學(xué)理.files/image310.gif)
學(xué)理.files/image312.gif)
學(xué)理.files/image314.gif)
(2)由⑴得:學(xué)理.files/image316.gif) ,
,
學(xué)理.files/image318.gif)
19.法一:(1)連接學(xué)理.files/image320.gif) ,設(shè)
,設(shè)學(xué)理.files/image322.gif) ,則
,則學(xué)理.files/image324.gif) 。
。
因為學(xué)理.files/image168.gif) ,所以
,所以學(xué)理.files/image326.gif) ,故
,故學(xué)理.files/image328.gif) ,從而
,從而學(xué)理.files/image330.gif) ,
,
故學(xué)理.files/image332.gif) 。
。
又因為學(xué)理.files/image334.gif) ,
,
所以學(xué)理.files/image336.gif) ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)學(xué)理.files/image338.gif) 取等號。
取等號。
此時學(xué)理.files/image340.gif) 為
為學(xué)理.files/image342.gif) 邊的中點,
邊的中點,學(xué)理.files/image178.gif) 為
為學(xué)理.files/image344.gif) 邊的中點。
邊的中點。
故當(dāng)學(xué)理.files/image178.gif) 為
為學(xué)理.files/image344.gif) 邊的中點時,
邊的中點時,學(xué)理.files/image180.gif) 的長度最小,其值為
的長度最小,其值為學(xué)理.files/image346.gif)
(2)連接學(xué)理.files/image348.gif) ,因為此時
,因為此時學(xué)理.files/image164.gif) 分別為
分別為學(xué)理.files/image166.gif) 的中點,
的中點,
故學(xué)理.files/image350.gif) ,所以
,所以學(xué)理.files/image352.gif) 均為直角三角形,
均為直角三角形,
從而學(xué)理.files/image354.gif) ,所以
,所以學(xué)理.files/image356.gif) 即為直線
即為直線學(xué)理.files/image184.gif) 與平面
與平面學(xué)理.files/image186.gif) 所成的角。
所成的角。
因為學(xué)理.files/image358.gif) ,所以
,所以學(xué)理.files/image360.gif) 即為所求;
即為所求;
(3)因學(xué)理.files/image330.gif) ,又
,又學(xué)理.files/image362.gif) ,所以
,所以學(xué)理.files/image364.gif) 。
。
又學(xué)理.files/image366.gif) ,故三棱錐
,故三棱錐學(xué)理.files/image190.gif) 的表面積為
的表面積為
學(xué)理.files/image369.gif) 。
。
因為三棱錐學(xué)理.files/image190.gif) 的體積
的體積學(xué)理.files/image371.gif) ,
,
所以學(xué)理.files/image373.gif) 。
。
法二:(1)因學(xué)理.files/image375.gif) ,故
,故學(xué)理.files/image377.gif) 。
。
設(shè)學(xué)理.files/image379.gif) ,則
,則學(xué)理.files/image381.gif) 。
。
所以學(xué)理.files/image383.gif) ,
,
當(dāng)且僅當(dāng)學(xué)理.files/image385.gif) 取等號。此時
取等號。此時學(xué)理.files/image178.gif) 為
為學(xué)理.files/image344.gif) 邊的中點。
邊的中點。
故當(dāng)學(xué)理.files/image178.gif) 為
為學(xué)理.files/image344.gif) 的中點時,
的中點時,學(xué)理.files/image180.gif) 的長度最小,其值為
的長度最小,其值為學(xué)理.files/image346.gif) ;
;
(2)因學(xué)理.files/image330.gif) ,又
,又學(xué)理.files/image362.gif) ,所以
,所以學(xué)理.files/image364.gif) 。
。
記學(xué)理.files/image178.gif) 點到平面
點到平面學(xué)理.files/image186.gif) 的距離為
的距離為學(xué)理.files/image387.gif) ,
,
因學(xué)理.files/image366.gif) ,故
,故學(xué)理.files/image389.gif) ,解得
,解得學(xué)理.files/image391.gif) 。
。
學(xué)理.files/image393.gif) 因
因學(xué)理.files/image395.gif) ,故
,故學(xué)理.files/image397.gif) ;
;
(3)同“法一”。
法三:(1)如圖,以學(xué)理.files/image138.gif) 為原點建立空間直角坐標(biāo)系,設(shè)
為原點建立空間直角坐標(biāo)系,設(shè)學(xué)理.files/image322.gif) ,則
,則學(xué)理.files/image400.gif) ,
,
所以學(xué)理.files/image336.gif) ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)學(xué)理.files/image338.gif) 取等號。
取等號。
此時學(xué)理.files/image340.gif) 為
為學(xué)理.files/image342.gif) 邊的中點,
邊的中點,學(xué)理.files/image178.gif) 為
為學(xué)理.files/image344.gif) 邊的中點。
邊的中點。
故當(dāng)學(xué)理.files/image178.gif) 為
為學(xué)理.files/image344.gif) 邊的中點時,
邊的中點時,學(xué)理.files/image180.gif) 的長度最小,其值為
的長度最小,其值為學(xué)理.files/image346.gif) ;
;
(2)設(shè)學(xué)理.files/image402.gif) 為面
為面學(xué)理.files/image186.gif) 的法向量,因
的法向量,因學(xué)理.files/image404.gif) ,
,
故學(xué)理.files/image406.gif) 。取
。取學(xué)理.files/image408.gif) ,得
,得學(xué)理.files/image410.gif) 。
。
又因學(xué)理.files/image412.gif) ,故
,故學(xué)理.files/image414.gif) 。
。
因此學(xué)理.files/image416.gif) ,從而
,從而學(xué)理.files/image418.gif) ,
,
所以學(xué)理.files/image397.gif) ;
;
(3)由題意可設(shè)學(xué)理.files/image420.gif) 為三棱錐
為三棱錐學(xué)理.files/image190.gif) 的內(nèi)切球球心,
的內(nèi)切球球心,
則學(xué)理.files/image422.gif) ,可得
,可得學(xué)理.files/image424.gif) 。
。
與(2)同法可得平面學(xué)理.files/image426.gif) 的一個法向量
的一個法向量學(xué)理.files/image428.gif) ,
,
又學(xué)理.files/image430.gif) ,故
,故學(xué)理.files/image432.gif) ,
,
解得學(xué)理.files/image434.gif) 。顯然
。顯然學(xué)理.files/image436.gif) ,故
,故學(xué)理.files/image438.gif) 。
。
20.解:(1)當(dāng)學(xué)理.files/image200.gif) 時,
時,學(xué)理.files/image440.gif) 。令
。令學(xué)理.files/image442.gif) 得
得學(xué)理.files/image444.gif) ,
,
故當(dāng)學(xué)理.files/image446.gif) 時
時學(xué)理.files/image448.gif) ,
,學(xué)理.files/image083.gif) 單調(diào)遞增;
單調(diào)遞增;
當(dāng)學(xué)理.files/image451.gif) 時
時學(xué)理.files/image453.gif) ,
,學(xué)理.files/image083.gif) 單調(diào)遞減。
單調(diào)遞減。
所以函數(shù)學(xué)理.files/image083.gif) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為學(xué)理.files/image455.gif) ,
,
單調(diào)遞減區(qū)間為學(xué)理.files/image457.gif) ;
;
(2)法一:因學(xué)理.files/image459.gif) ,故
,故學(xué)理.files/image461.gif) 。
。
令學(xué)理.files/image463.gif) ,
,
要使學(xué)理.files/image465.gif) 對滿足
對滿足學(xué)理.files/image203.gif) 的一切
的一切學(xué)理.files/image056.gif) 成立,則
成立,則學(xué)理.files/image467.gif) ,
,
解得學(xué)理.files/image469.gif) ;
;
法二:學(xué)理.files/image459.gif) ,故
,故學(xué)理.files/image461.gif) 。
。
由學(xué)理.files/image206.gif) 可解得
可解得學(xué)理.files/image472.gif) 。
。
因為學(xué)理.files/image474.gif) 在
在學(xué)理.files/image476.gif) 單調(diào)遞減,因此
單調(diào)遞減,因此學(xué)理.files/image478.gif) 在
在學(xué)理.files/image476.gif) 單調(diào)遞增,故
單調(diào)遞增,故學(xué)理.files/image480.gif) 。設(shè)
。設(shè)學(xué)理.files/image482.gif) ,
,
則學(xué)理.files/image484.gif) ,因為
,因為學(xué)理.files/image486.gif) ,
,
所以學(xué)理.files/image488.gif) ,從而
,從而學(xué)理.files/image490.gif) 在
在學(xué)理.files/image476.gif) 單調(diào)遞減,
單調(diào)遞減,
故學(xué)理.files/image492.gif) 。因此
。因此學(xué)理.files/image494.gif) ,即
,即學(xué)理.files/image469.gif) 。
。
(3)因為學(xué)理.files/image496.gif) ,所以
,所以學(xué)理.files/image498.gif)
即學(xué)理.files/image500.gif) 對一切
對一切學(xué)理.files/image212.gif) 恒成立。
恒成立。
學(xué)理.files/image502.gif) ,令
,令學(xué)理.files/image504.gif) ,
,
則學(xué)理.files/image506.gif) 。因為
。因為學(xué)理.files/image212.gif) ,所以
,所以學(xué)理.files/image508.gif) ,
,
故學(xué)理.files/image510.gif) 在
在學(xué)理.files/image512.gif) 單調(diào)遞增,有
單調(diào)遞增,有學(xué)理.files/image514.gif) 。
。
因此學(xué)理.files/image516.gif) ,從而
,從而學(xué)理.files/image518.gif) 。
。
所以學(xué)理.files/image520.gif) 。
。
21.解:(1)設(shè)學(xué)理.files/image522.gif) ,則由題
,則由題學(xué)理.files/image524.gif) ,
,
由學(xué)理.files/image526.gif) 得
得學(xué)理.files/image528.gif) ,故
,故學(xué)理.files/image530.gif) 。
。
又根據(jù)學(xué)理.files/image532.gif) 可得
可得學(xué)理.files/image534.gif) ,
,
即學(xué)理.files/image536.gif) ,代入可得
,代入可得學(xué)理.files/image538.gif) ,
,
解得學(xué)理.files/image540.gif) (舍負)。故
(舍負)。故學(xué)理.files/image178.gif) 的方程為
的方程為學(xué)理.files/image542.gif) ;
;
(2)法一:設(shè)學(xué)理.files/image544.gif) ,代入
,代入學(xué)理.files/image542.gif) 得
得學(xué)理.files/image547.gif) ,
,
故學(xué)理.files/image549.gif) ,
,
從而學(xué)理.files/image551.gif)
學(xué)理.files/image553.gif)
學(xué)理.files/image555.gif)
因此學(xué)理.files/image240.gif) 。
。
法二:顯然點學(xué)理.files/image142.gif) 是拋物線
是拋物線學(xué)理.files/image178.gif) 的焦點,點
的焦點,點學(xué)理.files/image558.gif) 是其準(zhǔn)線
是其準(zhǔn)線學(xué)理.files/image560.gif) 上一點。
上一點。
設(shè)學(xué)理.files/image138.gif) 為
為學(xué)理.files/image344.gif) 的中點,過
的中點,過學(xué)理.files/image564.gif) 分別作
分別作學(xué)理.files/image560.gif) 的垂線,垂足分別為
的垂線,垂足分別為學(xué)理.files/image566.gif) ,
,
則學(xué)理.files/image568.gif) 。
。
因此以學(xué)理.files/image344.gif) 為直徑的圓與準(zhǔn)線
為直徑的圓與準(zhǔn)線學(xué)理.files/image560.gif) 相切(于點
相切(于點學(xué)理.files/image570.gif) )。
)。
若學(xué)理.files/image558.gif) 與
與學(xué)理.files/image570.gif) 重合,則
重合,則學(xué)理.files/image572.gif) 。否則點
。否則點學(xué)理.files/image558.gif) 在
在學(xué)理.files/image574.gif) 外,因此
外,因此學(xué)理.files/image576.gif) 。
。
綜上知學(xué)理.files/image240.gif) 。
。
22.證明:(1)因學(xué)理.files/image578.gif) ,故
,故學(xué)理.files/image580.gif) 。
。
顯然學(xué)理.files/image582.gif) ,因此數(shù)列
,因此數(shù)列學(xué)理.files/image245.gif) 是以
是以學(xué)理.files/image584.gif) 為首項,以2為公比的等比數(shù)列;
為首項,以2為公比的等比數(shù)列;
(2)由⑴知學(xué)理.files/image586.gif) ,解得
,解得學(xué)理.files/image588.gif) ;
;
(3)因為
學(xué)理.files/image590.gif)
所以學(xué)理.files/image592.gif) 。
。
又學(xué)理.files/image594.gif)
學(xué)理.files/image596.gif) (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)學(xué)理.files/image598.gif) 時取等號),
時取等號),
故學(xué)理.files/image600.gif) 。
。
綜上可得學(xué)理.files/image252.gif) 。(亦可用數(shù)學(xué)歸納法)
。(亦可用數(shù)學(xué)歸納法)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com